Режим - движение - частица
Cтраница 1
Режимы движения частиц с постоянным контактом с рабочим органом применяются при дозировании крошки каучука. Эти режимы могут быть с успехом применены при предварительной обработке материала, а также в том случае, если по технологическим требованиям необходимо исключить относительное движение частиц друг относительно друга. [1]
 |
Сферодайзер. / - корпус. 2 - лопатки. 3 - роликовые станины. [2] |
Такой режим движения частиц обусловлен рациональной конструкцией лопаток и правильным их расположением. [3]
Отличительной особенностью режимов движения частиц с подбрасыванием, применяемых в процессе сушки, является наличие свободного полета частицы над вибрирующей плоскостью. Рассмотрим уравнение движения частицы над плоскостью, когда на нее кроме вибрационных сил действует гидродинамическая сила потока. При рассмотрении реальной схемы кроме гидродинамических сил FK и FA действует еще знакопеременная относительно оси у сила сопротивления, пропорциональная скорости движения частиц; однако эта сила, абсолютные значения которой малы вследствие незначительных относительных скоростей между частицами и газом, не учитывается. [4]
При ла хошарном режиме движения частицы жидкости перемещаются по траекториям, направленным вдоль общего течения, в частности, вдоль оси трубы без поперечного перемешивания. [5]
Для установления отклонения режима движения частиц смешиваемых компонентов в реальном аппарате от идеального, описываемого потоками идеального смешения или вытеснения, необходимо сравнить соответствующие кривые функций распределения времени пребывания в аппарате и их моменты. Наиболее распространенной характеристикой является второй момент - дисперсия [30], которая характеризует разброс рассматриваемой величины около среднего значения при непрерывном распределении для конечного числа эквидистантных точек. [6]
Следует иметь в виду, что процесс центробежного разделения, скорость и режим движения частицы с увеличением радиуса изменяются, но все расчеты проводят с учетом наибольшего фактора разделения. [7]
Подставив в уравнение ( 3) значение А, можно найти Wo для всех режимов движения частицы: ламинарный, переходный, турбулентный. [8]
При размерах частиц более 10 6 м поправкой Каннингхема пренебрегают, среду рассматривают как сплошную, а режим движения частиц называют гидродинамическим или стоксовским. [9]
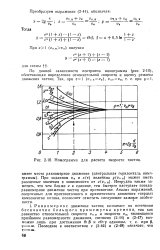 |
Номограмма для расчета скорости частиц. [10] |
По данной зависимости построена номограмма ( рис. 2 - 10), облегчающая определение относительной скорости и оценку режима движения частиц. [11]
Как следует из условия (4.34), наличие гидродинамической силы потока газа, отражающейся в величине степени взвешивания, сдвигает границу начала режима движения частицы без подбрасывания в сторону меньших значений параметров вибрации. [12]
Уравнение (6.25) было решено численно применительно к сферическому телу для двух предельных случаев, v рассмотренных выше ( Reo - op и Reol), в предположении стоксова режима движения частицы. Полученные результаты представлены на фиг. Установлено существование критического числа Сток-са, ниже которого коэффициент захвата равен нулю. [13]
Здесь вязкость vnT) n / p весьма условно оценена через плотность жидкости вместо плотности суспензии. Отсутствует учет влияния концентрации на с / за счет изменения режима движения частиц ( соударения, трение о стенки, изменение степени турбулентности потока и пр. Z) / da25 - b30, а для D / da25 - b30 согласование результатов не достигнуто. [14]
Здесь вязкость vn iln / P весьма условно оценена через плотность жидкости вместо плотности суспензии. Отсутствует учет влияния концентрации па с / за счет изменения режима движения частиц ( соударения, трение о стенки, изменение степени турбулентности потока и пр. D / d325 - H30, а для D / da25 - f - 30 согласование результатов не достигнуто. [15]
Страницы: 1 2