Стационарный режим - колебание
Cтраница 1
Стационарный режим колебаний устойчив, если при малых отклонениях система стремится в прежнее состояние. Вернемся к укороченным уравнениям для нестационарного режима и рассмотрим поведение системы при малых возмущениях. [1]
Рассмотрена методика определения стационарного режима колебаний СВЧ генератора на туннельном диоде по годографам последнего, построенным на круговых диаграммах. [2]
Рано или поздно наступает стационарный режим колебаний, при котором подводимая энергия в точности компенсируется джоулевыми потерями. [3]
Рассмотрим теперь, как происходит установление стационарного режима колебаний в изучаемой модели автоколебательной системы и чем определяется значение амплитуды. Начнем с наиболее простого случая: брусок в начальный момент покоится в положении, соответствующем недеформированной пружине. Точка, изображающая такое начальное состояние, находится в начале координат на фазовой плоскости. [4]
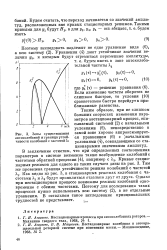 |
Зоны существования автоколебаний и граница устойчивости колебаний с частотой Ал. [5] |
Как видно из рис. 3, в стационарных режимах колебания с частотами K. Однако при нестационарном процессе возможны режимы колебаний одновременно с обеими частотами. Поэтому для исследования таких процессов нужно использовать всю систему ( 2), а не отдельные уравнения. В остальном такое исследование принципиальных трудностей не представляет. [6]
Последнее содержит характеристику двигателя L ( Q), таким образом стационарные режимы колебаний становятся зависящими от свойств источника энергии. Нетрудно видеть, что система уравнений ( 2) и ( 3) может иметь несколько решений. Каждое из решений должно быть исследовано на устойчивость. [7]
 |
Энергетические соотношения. [8] |
Начальная фаза автоколебаний произвольна, поскольку произволен момент самовозбуждения и установление стационарного режима колебаний. [9]
Такое состояние системы также относится к установившемуся, а режим называют стационарным режимом колебаний. [10]
Как видно из рис. 9.3.2, с течением времени шар выходит на стационарный режим колебаний. [11]
Математическая модель в виде (1.5) непосредственно используется при анализе переходных процессов, устойчивости, стационарных режимов колебаний. Эта же модель позволяет решать и задачи анализа статических состояний. [12]
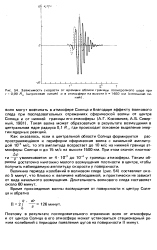 |
Зависимость скорости от времени вблизи границы политропного шара при г 0 99 R ( штриховая линия и в атмосфере на высоте h - 1460 км ( сплошная линия. [13] |
Поэтому в результате последовательного отражения волн от атмосферы и от центра Солнца в его атмосфере может установиться стационарный режим колебаний с периодом появления цугов на поверхности II минут. [14]
А, В, С зависят от времени; 2) элементы матриц AI, В, С постоянны, но время процесса ограничено и система не успевает выйти на установившийся стационарный режим колебаний. [15]
Страницы: 1 2