Статический режим

Cтраница 3

Рассмотрим статический режим схемы на рис. 3 - 1 при следующих условиях, упрощающих анализ. [31]

Статические характе - связывающую Хст и FCT. Для прибли-ристики нелинейных САУ. женной оценки можно оперировать. [32]

Рассмотрим вначале статический режим нелинейных статических САУ. Статический режим САУ определяется зависимостью статического значения выходной величины Хст системы от статического значения внешнего воздействия FCT. В нелинейных системах наличие нелинейных статических характеристик у отдельных звеньев приводит к тому, что зависимость Хст от Fc получается также нелинейной. В последнем случае зависимость может быть неоднозначной, как и показано на рисунке, если в систему входит звено с соответственно неоднозначной характеристикой. [33]

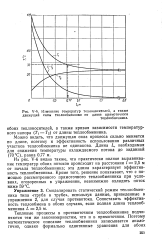Изменение температур теплоносителей, а также движущей силы теплообменника по длине прямоточного. [34]

Смоделировать статический режим теплообменника типа труба в трубе, используя данные, приведенные в упражнении 2, для случая противотока. [35]

Рассмотрим статический режим протекания непрерывного процесса. [36]

Рассматривается статический режим схемы симметричного триггера с непосредственными связями на полевых транзисторах с изолированным затвором и индуцированным каналом. Анализируются условия запирания и открывания транзисторов, нагрузочная способность, амплитуда выходного сигнала, потребляемая мощность. Приводится методика расчета статического режима триггера на заданную амплитуду импульса. [37]

Определение статического режима, данное ранее ( см. § 1.2), справедливо и для объекта регулирования. Особенности поведения объекта в статическом режиме зависят от его статических свойств ( см. § VI.2), отображаемых его статическими характеристиками, аналитическое выражение которых представляет собой уравнение статики объекта. Так как в реальных условиях любой объект регулирования находится под влиянием нескольких воздействий, его свойства можно иллюстрировать разными статическими характеристиками и разными уравнениями статики. [38]

Определение регулярных динамических и статических режимов.| Характер изменения температуры тела в регулярных динамических режимах при различных исходных данных. [39]

Расчет статических режимов может быть выполнен по методике, разработанной под руководством проф. [40]

Расчет статического режима в ПАЭС-1 заменен анализом установившихся значений токов и напряжений в конце переходного процесса. [41]

Для статического режима определяется угловая характеристика М / ( 0) как зависимость статического момента ШД при постоянных токах в обмотках статора от угла рассогласования ( или поворота) в электрических градусах оси полюсов ротора относительно положения устойчивого равновесия. [42]

Анализ статических режимов сводится к решению систем АУ. Для решения АУ применяют итерационные методы, основные характеристики которых - сходимость и скорость сходимости к точному решению. В САПР применяют в основном методы простой итерации, Ньютона и релаксационные. Методы простой итерации и релаксационные имеют линейную скорость сходимости и требуют небольших вычислительных затрат на одну итерацию. Эти методы применяются в основном для решения систем АУ большой размерности. Метод Ньютона имеет квадратичную скорость сходимости, но в общем случае сходится только в окрестности точного решения. Для расширения области сходимости метода Ньютона применяются метод продолжения решения по параметру и метод дифференцирования по параметру. Метод Ньютона и его модификации сводятся к решению систем ЛАУ на каждой итерации. Для решения систем ЛАУ наиболее широко применяют метод Гаусса и LU-разложения. Для систем ЛАУ большой размерности эти методы эффективны только при учете разреженности матриц коэффициентов. [43]

Структурная схема двухуровневой. [44]

Оптимизация статических режимов производится на основе статической математической модели объекта управления. Такой прием называется декомпозицией и оказывается эффективным, а иногда и единственно возможным для решения задачи оптимального управления сложным объектом. [45]

Страницы: 1 2 3 4