Значение - поправочная функция
Cтраница 1
Значения поправочной функции / зависят от размеров пластины, в которой находится трещина, размеров самой трещины, а также способа нагружения. [1]
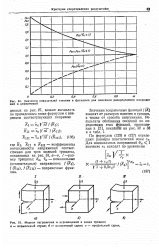 |
Значения показателей степени в функциях для описания распределения напряжен вий и деформаций.| Модели нагружения и перемещений в зонах трещин. [2] |
Значения поправочных функций / ( / С) зависят от размеров пластин и трещин, а также от способа нагружения. [3]
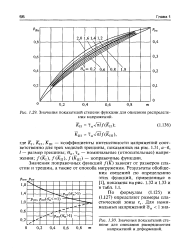 |
Значения показателей степени функции для описания распределения напряжений.| Значения показателей степени для описания распределения напряжений и деформаций. [4] |
Значения поправочных функций f ( K) зависят от размеров пластин и трещин, а также от способа нагружения. [5]
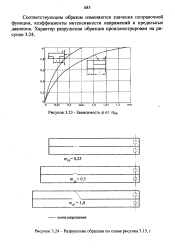 |
Зависимость ф от тсв.| Разрушение образцов по схеме рисунка, г. [6] |
Соответствующим образом изменяются значения поправочной функции, коэффициенты интенсивности напряжений и предельные давления. [7]
Проведенные расчеты показали, что значения поправочной функции Ак меняются в пределах от 0 4 до 0 9, причем большое значение имеет наличие или отсутствие пластичных пород в кровле пласта. Характерным для пластов большой мощности ( 500 - 1000 м) является большой размах колебаний значений кор-ректирупцей функции по объему залежи. [8]
Если для одной из моделей известно значение поправочной функции, то по экспериментальной зависимости ср стнпр. [9]
Тогда на основе формулы (9.27), принимая значение поправочной функции на длину трещины равной единице, получаем для длины трещины 33 мм оценку уровня эквивалентного напряжения около 240 МПа. Полученная оценка является несколько завышенной, так как длина трещины и форма фронта указывают на необходимость использования в расчетах поправочной функции более единицы. [10]
Выявленное несоответствие результатов моделирования экспериментальным данным показало необходимость корректировки значений поправочной функции (6.41) применительно к этапу роста трещины после многопараметрических однократных переходов. [11]
 |
К методике определения интенсивности деформаций в упругопластической стадии нагружения соединений с порами. [12] |
Нейбера дает завышенные значения местных напряжений и деформаций в упругопластической области. Значение данной поправочной функции в каждом конкретном случае находят численно или экспериментально. [13]
 |
Схема возникновения сдвига фаз на угол Их в случае синусоидального двухосного нагружения образца по двум независимым осям. [14] |
Соблюдение условий подобия в анализе экспериментальных данных по стадиям роста трещины с учетом эффекта ее туннелирования позволяет продемонстрировать эффективность использования единой кинетической кривой для моделирования роста усталостных трещин на примере алюминиевых сплавов. Переход к другим материалам не требует проведения столь обширного эксперимента для уточнения или дополнительной корректировки значений поправочных функций. [15]
Страницы: 1 2