Значение - интегральная функция
Cтраница 1
Значения интегральных функций при данной аппроксимации следует брать по таблице, иначе значения аргумента могут выйти за пределы аппроксимации. [1]
Значения интегральной функции % 2 - распределения ( xjt. [2]
Так как значение интегральной функции распределения Ф2 ( у) следует взять при у оа [, то в выражении (5.49) вместо о 1Д следует подставить аа. [3]
Полученные таким образом значения интегральной функции распределения заносят в последнюю графу составленной таблицы. [4]
 |
Значения функций Фи. Ф и Фир при ц 0 5 и К 1 2.| Схема размеров, перемещений и усилий оболочки вращения. [5] |
В последовательных приближениях определяют значения интегральных функций пластичности для последовательно вычисляемых значений деформаций. [6]
 |
Функции распределения. [7] |
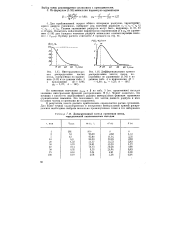
На рис. 3.1, а значение интегральной функции в точке X численно равно вероятности того, что случайная величина X, в результате i - ro наблюдения окажется левее точки X, При перемещении точки X вдоль оси ОХ эта вероятность будет, очевидно, изменяться, но она не может уменьшиться при перемещении точки X вправо. Поэтому интегральная функция распределения является неубывающей функцией аргумента. Практически разрешающая способность измерительных средств делит всю область значений измеряемой величины на отрезки, в пределах которых наблюдатель не различает изменения измеряемой величины. Поэтому в пределах каждого отрезка интегральная функция распределения сохраняет постоянное значение и скачкообразно изменяется при переходе границы на некоторое конечное значение. [8]
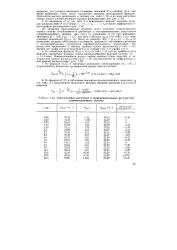 |
Сопоставление расчетных и экспериментальных результатов седиментационного анализа. [9] |
Для этих вновь выбранных точек также определяют значения интегральной функции. [10]
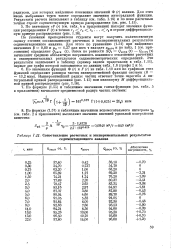 |
Сопоставление расчетных и экспериментальных результатов седиментационного анализа. [11] |
Для этих вновь выбранных точек также определяют значения интегральной функции. Результаты расчета записывают в таблицу ( см. табл. 1.10) и по всем расчетным точкам строят соответствующую кривую распределения ( ом. [12]
Находится максимальная разность значений между теоретическим и статистическим значениями интегральной функции распределения. [13]
По известным значениям храсч и 3 из табл. 3 ( см. приложение) находят значения интегральной функции распределения Ф ( / /) Может оказаться, что начиная с какого-то определенного радиуса интегральная функция принимает отрицательные значения. Это показывает, что частиц данного радиуса и всех больших частиц в суспензии не содержится. [15]
Страницы: 1 2