Значение - интегральная функция
Cтраница 2
Если рассматривать результат отдельного наблюдения Xi как случайную точку на оси Ох ( рис. 11), то значение интегральной функции распределения в точке х численно равно вероятности то-рис. [16]
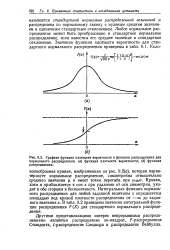 |
Графики функции плотности вероятности и функции распределения для нормального распределения, ( а функция плотности вероятности. ( Ь функция распределения. [17] |
Кривая, хотя и приближается к оси х при удалении от оси симметрии, уходит в обе стороны в бесконечность. В табл. 9.2 приведены значения интегральной функции распределения F ( X) для стандартного нормального распределения. [18]
Для определения динамики показателей заводнения пласта этой переменной следует задаваться, а значения интегральной функции F ( L) можно снимать с фактического графического изображения распределения микропотоков по приведенной длине при вычислении интегралов приближенным методом Симпсона или трапеций. [19]
Установив гмакс и гмин - предельные значения радиусов частиц суспензии, на кривой седиментации выбирают ряд точек в местах наибольшего изменения кривизны. Таким образом, исследуемую суспензию разбивают на несколько фракций, в данном случае па пять. Далее проводят касательную к кривой в одной из выбранных точек, например в точке С, и прямую, параллельную оси абсцисс. В осадке находятся частицы всех размеров, как крупные, так и мелкие, которые к началу анализа находились вблизи чашки весов. Частицы, которые за время тх прошли путь Н от поверхности жидкости до чашечки весов [ их радиус г4 может быть вычислен по уравнению (1.45) 1, а также все более крупные частицы ко времени тг осядут полностью и их в суспензии не останется. Она равна Ф ( тх) - значению интегральной функции распределения в точке тх. [20]
Установив гыакс и гмин - предельные значения радиусов частиц суспензии, на кривой седиментации выбирают ряд точек в местах наибольшего изменения кривизны. Таким образом, исследуемую суспензию разбивают на несколько фракций, в данном случае на пять. Далее проводят касательную к кривой в одной из выбранных точек, например в точке С, и прямую, параллельную оси абсцисс. Отрезок 00 численно равен массе Q ( тг) всех частиц, осевших ко времени тх. В осадке находятся частицы всех размеров, как крупные, так и мелкие, которые к началу анализа находились вблизи чашки весов. Частицы, которые за время тх прошли путь Н от поверхности жидкости до чашечки весов [ их радиус г4 может быть вычислен по уравнению (1.45) ], а также все более крупные частицы ко времени тх осядут полностью и их в суспензии не останется. Она равна Ф ( тх) - значению интегральной функции распределения в точке TJ. [21]
Страницы: 1 2