Значение - данная функция
Cтраница 1
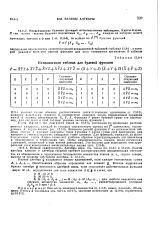 |
Истинностная таблица для булевой функции. [1] |
Значения данной функции F из истинностной таблицы вносят ъ нужные квадраты; тогда функция F равна сумме всех одночленов, для которых в соответствующих квадратах стоит единица. Для функций, пожалуй, до шести переменных карта Карно позволяет удобным образом перегруппировать эти одночлены в объединения и пересечения так, чтобы минимизировать, скажем, число логических сложений, умножений и / или взятия дополнений. [2]
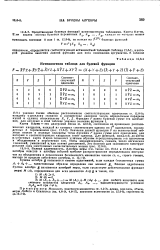 |
Истинностная таблица для булевой функции. [3] |
Значения данной функции F из истинностной таблицы вносят в нужные квадраты; тогда функция F равна сумме всех одночленов, для которых в соответствующих квадратах стоит единица. Для функций, пожалуй, до шести переменных карта Карно позволяет улобным образом перегруппировать эти одночлены в объединения и пересечения так, чтобы минимизировать, скажем, число логических сложений, умножений и / или взятия дополнений. [4]
А) Значения данных функций и их производных любого порядка при х 0 были вычислены ранее в решении задачи 297 ( гл. [5]
Функция, обратная по значениям данной функции. [6]
Поверхность, в каждой точке которой значение данной функции постоянно, называется поверхностью уровня. [7]
Знак у нуля говорит о том, что значение данной функции берется при подходе к нулю справа. [8]
Относительно большую точность имеют симметрические формулы дифференцирования, учитывающие значения данной функции у как при х д: 0, так и при х С ха. Эти формулы обычно называются центральными формулами дифференцирования. [9]
Если какое - ибо определение или соотношение между значениями данных функций выполнены для каждого со из множества А с Q, то мы говорим, что это определение или соотношение выполняется на А; при этом мы будем опускать выражение на Л, если А И. [10]
Найти допустимые абсолютные погрешности аргументов, которые позволяют вычислять значения данных функций с четырьмя верными знаками. [11]
В задачах 1185 - 1197 найти наибольшие и наименьшиг значения данных функций на указанных отрезках п в указанных интервалах. [12]
Часто требуется, чтобы максимум абсолютной величины разности между значениями данной функции [ ( л) и значениями многочлена Р ( х) не превосходил некоторой определенной величины, которую можно считать мерой приближения. [13]
Рациональная функция, значения которой в ряде точек совпадают со значениями данной функции, называется многоточечной аппроксимацией Паде. Соответствующая общая задача интерполяции рациональными функциями называется задачей Коши - Якоби. Многоточечные аппроксимации Паде называют также рациональными интерполяциями, yV - точечными аппроксимациями, ЛЛточеч-ными аппроксимациями Паде или аппроксимациями Ньютона - Паде в зависимости от контекста. В случае кратных точек ( узлов) интерполяции иногда говорят об осцилляторной интерполяции. [14]
Окончив работу по составлению уравнений, проверьте себя, вычислив по составленным уравнениям таблицу значений данной функции во внутренних точках интервалов разбиения. [15]
Страницы: 1 2 3