Значение - энергия - решетка
Cтраница 1
 |
Энергии решетки ( кДж / моль. [1] |
Значения энергий решетки многих кристаллов приведены в табл. 9.3 наряду со значениями, полученными косвенным путем из термохимических данных с использованием цикла Борна-Габера. [2]
Значения энергии решетки инертных газов, вычисленные по формуле (5.25), довольно хорошо согласуются с экспериментально определяемой теплотой сублимации Qcy6 при температуре 70 К, вблизи которой С / реш должна быть меньше, чем Qcy6 на величину нулевой энергии. [3]
 |
Результаты расчетов теплоты образования гексафторосиликатов ккал. [4] |
Использование значений энергий решеток фторидов, опубликованных позднее С. А. Барковым [154], не вносит существенных изменений в результаты расчетов. [5]
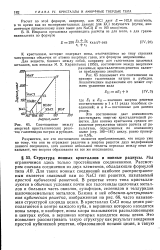 |
Соотношение между энергией кристаллических решеток галогенидов натрия и рубидия. [6] |
Ец - значения энергии решетки соответственно в I и II рядах подобных соединений; а и Ь - постоянные для данных рядов. [7]
Очень хорошее совпадение значений энергии решетки, вычисленных из известных теплот образования и других величин при помощи цикла Борна и определенных в предположении чисто ионной структуры, дает существенное подтверждение того, что дифториды переходных металлов обладают преимущественно свойствами ионных соединений. Точные значения энергии решетки для три - и тетрафторидов, к сожалению, отсутствуют, а термохимические данные для этих соединений весьма скудны. [8]
В табл. 46 приведены значения энергий решеток для некоторых типичных соединений щелочноземельных металлов. Эти значения не особенно точны, но они монотонно уменьшаются с ростом ионного радиуса катиона. [9]
В табл. 34 приведены значения энергии решетки галогенидов и гидроокисей некоторых элементов третьей группы. AIX, и вычисленных по данным работы [3], не превышают 2 ккал. Значения С ме ( ОН), менее точны; отметим, что для большинства гидроокисей они были найдены косвенным путем, так как теплоты образования известны только для четырех веществ [3], причем для А1 ( ОН) 3 и Т1 ( ОН) 3 они представляются сомнительными. [10]
Число состояний, соответствующих значению энергии решетки Ер ( или заселенность уровней в решетке), описывается распределением Больцмана. [11]
 |
Энергия решеток ( кДж / моль, вычисленная по формуле Капустинского. [12] |
Из табл. 1.3 видно, что значения энергии решетки, вычисленные по формулам Капустинского, близки к энергиям решеток, найденным экспериментальным путем. Следует заметить, что формула (1.9) с уменьшением степени ионности становится более корректной. [13]
Из (1.4) можно вычислить теоретическое, значение энергии решетки; полученные таким образом значения хо-согласуются с экспериментальными значениями, определенными с помощью цикла Борна-Габера. [14]
Тем не менее сравнение устойчивости минералов по значениям энергий решеток, особенно при использовании относительных величин, дает результаты, которые согласуются с экспериментом. Это объясняется тем, что энергию решетки можно рассматривать в качестве косвенной характеристики прочности химической связи. Именно поэтому удается использовать энергии решеток при рассмотрении процессов разложения и растворения минералов. [15]
Страницы: 1 2 3