Значение - энтропия
Cтраница 1
Значение энтропии характеризует степень неупорядоченности системы, служит количественной мерой этой неупорядоченности. [1]
Значение энтропии зависит от массы или от количества вещества, следовательно, подобно внутренней энергии и энтальпии, энтропия является экстенсивной физической величиной. [2]
Значение энтропии зависит от массы системы. [3]
Значения энтропии при температурах, близких к абсолютному нулю, необходимы для решения практических и теоретических термохимических задач, и это в значительной степени стимулировало появление дополнительного постулата, так называемого третьего закона термодинамики. В 1906 г. Нернст [1053] пришел к выводу, что изменение энтропии химической реакции вблизи абсолютного нуля пренебрежимо мало. В 1912 г. Планк [1168] показал, что кристаллическая решетка индивидуального вещества при абсолютном нуле характеризуется максимальной степенью упорядоченности и в связи с этим должна обладать нулевой энтропией. Симон [1350] и позднее Уилкс [1613] рассмотрели развитие этой концепции начиная с тепловой теоремы Нернста и до наших дней. [4]
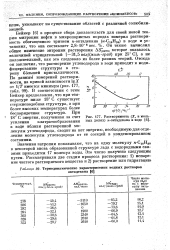 |
Термодинамические характеристики водных растворов.| Растворимость ( X, в мольных долях н-октадекана в воде. [5] |
Значения энтропии показывают, что на одну молекулу к - С18Н38 в некоторой вновь образованной структуре льда с водородными связями приходится 17 молекул воды. Это число получено следующим путем. [6]
Значение энтропии можно рассматривать как показатель большего или меньшего приближения изолированной системы к равновесному состоянию, а значит, и возможности протекания в ней термодинамических процессов. [7]
Значения энтропии оценены авторами в соответствии со структурными параметрами. [8]
Значение энтропии подсчитано по уравнению ( 85) при 7273 К ( см. стр. [9]
 |
Схема теиловой машины по второму началу термодинамики. [10] |
Значение энтропии можно легко определить только для состояния идеального газа. [11]
Значения энтропии для важнейших газов и их смесей, подсчитанные по особым формулам ( см. дальше), сводятся в таблицы. [12]
Значения энтропии при температурах, близких к абсолютному нулю, необходимы для решения практических и теоретических термохимических задач, и это в значительной степени стимулировало появление дополнительного постулата, так называемого третьего закона термодинамики. В 1906 г. Нернст [1053] пришел к выводу, что изменение энтропии химической реакции вблизи абсолютного нуля пренебрежимо мало. В 1912 г. Планк [1168] показал, что кристаллическая решетка индивидуального вещества при абсолютном нуле характеризуется максимальной степенью упорядоченности и в связи с этим должна обладать нулевой энтропией. Симон [1350] и позднее Уилкс [1613] рассмотрели развитие этой концепции начиная с тепловой теоремы Нернста и до наших дней. [13]
Значение энтропии 5 системы ( по существу соли) при температуре Т может быть вычислено как функция Я / TV Повторные размагничивания позволяют определить кривую зависимости энтропии 5 от сопротивления К, а следовательно, и значения dS / clR при Я-О. Термометр при соответствующих условиях может быть использован одновременно как нагреватель. [14]
Значение энтропии, которым нужно пользоваться, зависит от того, какими сведениями о системе мы располагаем, и на примере смешения компонентов что наглядно видно. Если бы мы считали, что энтропия смешения компонентов является объективным свойством системы безотносительно к нашему уровню наблюдения, то столкнулись бы со следующей ситуацией. Представим себе, что разность атомных весов двух изотопов может меняться непрерывно. Эта ситуация известна под названием парадокса Гиббса. [15]
Страницы: 1 2 3 4