Параметрический резонанс

Cтраница 1

Параметрический резонанс, в отличие от обычного, имеет две существенные особенности. [1]

Параметрический резонанс имеет место также при частотах v изменения параметра системы, близких к значениям вида 2ш0 / / х, где п - любое целое число. Так же уменьшаются и значения показателя усиления колебаний в них. [2]

Параметрический резонанс имеет место также при частотах у изменения параметра системы, близких к значениям вида 2сио / тг, где п - любое целое число. Так же уменьшаются и значения показателя усиления колебаний в них. [3]

Параметрические резонансы могут возникнуть на ряде собственных частот диффузора, сильно ухудшая качество излучаемого звука. Применением конуса с криволинейной образу-ющей можно резко уменьшить число и ампли - не кое возбужденл ре-туду возбуждения параметрических резонан - зонансов диффузора сов. Для уменьшения таких искажений и получения более равномерной частотной характеристики чувствительности широко применяются диффузоры не с круглым, а с эллиптическим большим основанием. [4]

Параметрический резонанс, для которого в ( 31) k ф /, называется комбинационным. Покажем, что при условии ( 31) для сколь угодно малых значений е может существовать область неустойчивости, и найдем ее границы с точностью до первой степени е включительно. [5]

Параметрический резонанс при - малых в наступает вблизи значений б / с 2 / 4, где k - целое положительное число. [6]

Параметрический резонанс характерен тем, что резонансные частоты не являются изолированными точками в пространстве параметров, а колебания системы могут нарастать по экспоненциальному закону с показателем, пропорциональным амплитуде возмущения. Задаче отыскания таких опасных множеств в пространстве параметров е, со и посвящена настоящая работа. Для более точной формулировки задачи введены некоторые обозначения и определения. [7]

Параметрический резонанс в системе ( 1) возможен, если матрица Q0 вырождена. [8]

Схема к вычислению входных сопротивлений относительно точки несимметрии. [9]

Параметрический резонанс является резонансом особого рода, при котором посторонняя механическая сила принудительно изменяет один из параметров контура ( емкость или индуктивность) против сил электромагнитного поля и, производя при этом работу, сообщает контуру дополнительную электромагнитную энергию. Источники электродвижущей силы и тока в контуре могут отсутствовать. Такое явление может возникнуть при работе электрической машины переменного тока иа емкость сети. Например, при вращении турбиной ротора генератора при каждом уменьшении индуктивности фазы и вследствие сохранения потокосцеплений и соответственного увеличения тока увеличивается запас энергии магнитного поля этой фазы. Эта энергия в колебательном процессе переходит в энергию электрического поля емкости сети и приводит соответственно к повышению напряжения на емкости. [10]

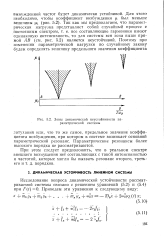Зоны динамической неустойчивости параметрической системы. [11]

Параметрические резонансы более высокого порядка не рассматриваются. [12]

Этим параметрический резонанс в линейной системе отличается от вынужденных колебаний при силовом воздействии, где поступление энергии пропорционально первой степени амплитуды, а потери - по-прежнему квадрату амплитуды, что приводит, как мы видели, к конечной амплитуде установившихся вынужденных колебаний. При параметрическом резонансе рост амплитуды ограничен только нелинейными свойствами колебательной системы. [13]

Явление параметрического резонанса имеет место не только в механических, но и в электрических системах. [14]

Изучение параметрического резонанса в сингулярно возмущенных системах по инициативе Ю. С. Колесова начато в заметке [56], в которой исследовались параболические системы типа реакция-диффузия с малыми коэффициентами диффузии. В дальнейшем эта тематика развивалась в работах [47, 83, 88, 77], посвященных, главным образом, анализу параметрических колебаний в случае сингулярно возмущенных телеграфных уравнений. [15]

Страницы: 1 2 3 4