Скачкообразный резонанс

Cтраница 1

Скачкообразный резонанс или, по терминологии Мандельштама и Папалек-си [69], резонанс 1-го рода, исследован во многих работах. Большое число работ посвящено анализу уравнения Дуффинга [20, 68, 104]; в них исследовалась частотная характеристика и If показывалось, что она имеет падающий участок. [1]

Такой скачкообразный резонанс, захватывающий линейный режим, был назван выше существенным. [2]

Кроме скачкообразного резонанса, причиной возникновения генерации сложного вида колебаний могут быть и субгармоники. [3]

Параметры скачкообразного резонанса, полученные графическим методом, достаточно хорошо согласуются с аналитическими и экспериментальными данными А. [4]

При скачкообразном резонансе неустойчивость в малом имеет место лишь в процессе скачка. Если Е п велико, то величина Я для токов той частоты, которая удовлетворяет условию генерации при отсутствии входного сигнала, мала и условие генерации не удовлетворяется. Если же Е п мало, то возникшая во время скачка из-за неустойчивости в малом генерация приводит к генерации и после скачка, так как малый внешний сигнал не меняет существенно величину Я на частоте генерации. [5]

При скачкообразном резонансе происходят скачки не только амплитуды, но и фазы выходного сигнала системы. [6]

Таков механизм скачкообразного резонанса, возбужаеыого изменением амплитуды. [7]

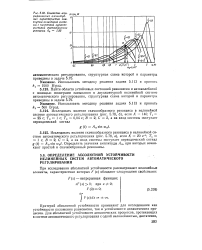Семейство логарифмических амплитудных характеристик замкнутой нелинейной системы с нанесенной характеристикой скачкообразного резонанса Ай 1 85. [8]

Исследовать явление скачкообразного резонанса в нелинейной системе автоматического регулирования ( рис. 5.78, в), если К 20 с 1; 7 1 с; В 2; С 2, а на вход системы поступает периодический сигнал g ( t) Л о sin со0Л Определить значения амплитуды А0, при которых возникают простой и скачкообразный резонансы. [9]

Как было показано, скачкообразный резонанс е может иметь место при запасе устойчивости по фазе, больше 90, что соответствует средней крутизне слада, большей 6 дБ / окт. Более высокие гармоники в силу тех же причин ослабляются в еще большей степени. [10]

Очевидно, что явление скачкообразного резонанса возможна только при таких Е, при которых вычисленное по (3.11) значение - cos ф меньше единицы. [11]

При этом важнейшей характеристикой скачкообразного резонанса служит величина Е п, показывающая, насколько скачки захватывают рабочий диапазон амплитуд сигналов. [12]

Величина скачков выходного сигнала при скачкообразном резонансе невелика. В рабочем диапазоне частот Еп 0 8, за рабочим диапазоном частот Е 0 6, что указывает на достаточно большую величину запасов устойчивости. [13]

Если в контурах местной обратной связи скачкообразный резонанс отсутствует, то амплитуды сигнала в различных местах тракта обратной связи будут однозначно зависеть от амплитуды сигнала Е в точках разрыва тракта обратной связи. [14]

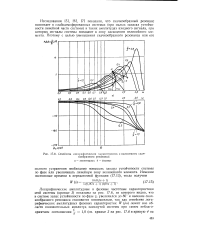Семейства логарифмических характеристик с выявлением скачкообразного резонанса. [15]

Страницы: 1 2 3