Сферический резонатор

Cтраница 1

Многослойный сферический резонатор находит широкое применение в различных радиофизических приложениях, например, в прецезионной измерительной аппаратуре сантиметрового диапазона. Рассмотрим падение плоской волны, распространяющейся вдоль оси z декартовой системы координат, начало которой совпадает с центром симметрии сферического резонатора. Запишем поле в / с-м слое в виде ( ср. [1]

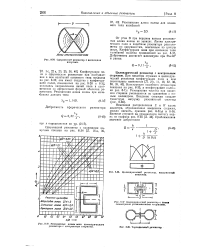
Открытый объемный резонатор с плоскими прямоугольными зеркалам ( Фабри - Перо ( а, дифракционные потери в открытом резонаторе ( б. [2]

Конфокальные сферические резонаторы, у которых фокусы обоих отражающих зер кал лежат в одной точке ( рис. 2 - 95), имеют меньший уровень потерь на излучение, чем резонатор с плоскими зеркалами. [3]

Стенки сферического резонатора сделаны из однородного проводящего материала, обладающего проводимостью о. [4]

Стенки сферического резонатора сделаны из однородного проводящего материала, обладающего проводимостью а. [5]

В центре сферического резонатора с идеально проводящими стенками помещен бесконечно малый электрический диполь, направленный по радиусу. [6]

При JV0 6 конфокальный сферический резонатор имеет меньшие дифракционные потери и большие соотношения этих потерь для низших типов колебании по сравнению с плоскопараллельным. [7]

Основными колебаниями в сферическом резонаторе являются колебания Ецо и Нцо. [8]

Сферический резонатор с входящими конусами.| Цилиндрический резонатор, нагруженный.| ЗГ. Резонансные длины волн цилиндрического резонатора с центральным стержнем. [9]

Конфигурация поля в сферическом резонаторе при возбуждении в нем колебаний основного типа показана на рис. 8 - 33; она имеет сходство с конфигурацией полей, показанных на рис. 8 - 28 и 8 - 32, отличаясь направлением линий поля в соответствии со сферической формой оболочки резонатора. [10]

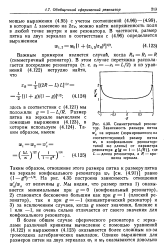Симметричный резонатор. Зависимость размера пятна ws на зеркале ( нормированного на. [11]

В более общем случае сферического резонатора с зеркалами различной кривизны вычисление с помощью уравнений (4.122) и выражения (4.123) оказывается более сложным из-за громоздких алгебраических выкладок. [12]

Физически неэквидистантность собственных частот сферического резонатора связана с дифракционными эффектами, вызывающими в области низких частот заметные отклонения от законов геометрической оптики. В частности, по концепции спиральных волн Времмера ( см. [ ПО ]) нормали к фазовым фронтам поля в сферическом резонаторе ( лучи) оказываются не прямыми, а спиральными линиями. Степень закрученности спирали возрастает С понижением частоты; при ш - оо спираль выпрямляется в обычный луч. [13]

Параметрический генератор на базе сферического резонатора предпочтительно использовать в нестационарном режиме. В начальный момент времени в резонаторе желательно возбудить колебания с частотами порядка 1 / т) 2, а затем спустя некоторое время, требуемое для распространения волны возбуждения по спектру до частот порядка I / TQI, воспользоваться высокоча-г стотным импульсом описанного типа. [14]

Устройство для ориентации ферромагнитного кристалла с поворотным электромагнитом. [15]

Страницы: 1 2 3 4