Сферический резонатор

Cтраница 3

Эта ширина кривой поглощения была измерена в волноводе со сферическим резонатором, расположенным на некотором расстоянии от металлических стенок. В обычных фильтрах ИЖГ резонаторы размещаются ближе к металлическим стенкам, и тогда возмущающее действие токов в стенках может уменьшить ненагруженную добротность до 2000 или меньше. Величина ЛЯ для данного типа материала обычно значительно меняется от образца к образцу в зависимости от того, до какой степени совершенна кристаллическая структура. [31]

Эта ширина кривой поглощения была измерена в волноводе со сферическим резонатором, расположенным на некотором расстоянии от металлических стенок. Величина ЛЯ для данного типа материала обычно значительно меняется от образца к образцу в зависимости от того, до какой степени совершенна кристаллическая структура. [32]

Учет высокочастотных потерь ограничивает спектр сигнала, генерируемого в сферическом резонаторе, точно так же, как в резонаторе одномерном. [33]

Несмотря на ряд упрощающих предположений, закон преобразования спектра в сферическом резонаторе, выраженный соотношениями ( 5.100 а), оказался достаточно сложным. Поэтому целесообразно остановиться более подробно на физическом анализе процессов, протекающих в низкочастотной и высокочастотной областях спектра. [34]

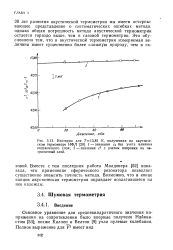Изотерма для Т 13 81 К, полученная на акустическом термометре НФЛ. / - значения а без учета влияния пограничного слоя. 2 - значения с2 с учетом поправки на пв-граничный слой. [35]

Вместе с тем последняя работа Молдовера [52] показала, что применение сферического резонатора позволяет существенно повысить точность метода. Возможно, что в конце концов акустическая термометрия оправдает возлагавшиеся на нее надежды. [36]

Применим теперь только что изложенный способ для определения радиуса корреляции поля сферического резонатора. [37]

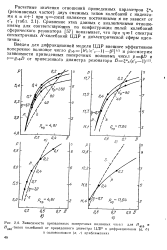Зависимости приведенных поперечных волновых чисел для Нolfi и. [38]

Сравнение этих данных с аналогичными отношениями для соответствующих по конфигурации полей колебаний сферического резонатора [57] показывает, что при цж спектры симметричных Я-колебаний ЦДР и диэлектрической сферы идентичны. [39]

Частота ш 2 74с / а есть наименьшая из всех собственных частот сферического резонатора. [40]

Следовательно, начиная с этих частот возможно эффективное параметрическое усиление поля в сферическом резонаторе и влияние дифракционного рассогласования оказывается преодоленным. [41]

Показать, что каждой собственной частоте ( fy & jc электромагнитных колебаний в сферическом резонаторе соответствует 2я 1 возможных типов колебаний. [42]

Частота ш - 2 74 с / а есть наименьшая из всех собственных частот сферического резонатора. [43]

Следовательно, в этой области спектра осуществление параметрической генерации на какой-либо паре собственных частот сферического резонатора не приводит к заметному возбуждению каких-либо других собственных колебаний и предположение (5.121) соответствует действительному положению вещей. Это, в принципе, открьшает возможность использования граничных поверхностей с резко выраженным минимумом потерь на упомянутых частотах. [44]

Зависимость коэффициента дифракционных потерь за проход от параметра Френеля для двух низших типов колебаний сферических резонаторов различной конфигурации показана на рис. 3.11, для цилиндрических резонаторов - на рис. 3.12. Для всех резонаторов дифракционные потери, естественно, возрастают с увеличением порядка моды и уменьшением параметра Френеля. Наименьшие дифракционные потери соответствуют конфокальному резонатору, а наибольшие - плоскому. [45]

Страницы: 1 2 3 4