Результат - численное интегрирование
Cтраница 1
Результаты численного интегрирования приведены в табл. 6 для цилиндрического сосуда и в табл. 7 - для сферического. [1]
Результаты численного интегрирования системы уравнений (3.2), (2.18) и (2.19) приводятся в виде сводных графиков т - N, причем к параметрам Q, л / и / V, по которым выбраны расчетные графики в предыдущей главе, добавляется по крайней мере еще один параметр v или vc, характеризующий переменную нагрузку. [2]
Результат численного интегрирования дифференциального уравнения как результат решения задачи приближенного анализа содержит погрешности. [3]
Однако результат численного интегрирования неточен вследствие ошибок измерений и неточности самого процесса интегрирования. Поэтому задаваясь несколькими рядами значений аир, усредняем х методом наименьших квадратов. [4]
Сравнение результатов численного интегрирования с аналитическим решением упрощенных уравнений показало, что частоты и амплитуды колебаний спутника и стабилизатора в обоих случаях практически совпадают. [5]
 |
Изменение теплового потока со временем. [6] |
Анализ результатов численного интегрирования показывает что для замороженных течений коэффициент теплоотдачи а, который определяется при известных тепловом потоке qw и температуре поверхности из закона Ньютона, слабо изменяется с течением времени. [7]
По результатам численного интегрирования системы (4.87) - (4.97) и из практики эксплуатации ПХГ и малых газовых месторождений известно, что давление в газоносной зоне практически постоянно. [8]
В результате численного интегрирования методом Рунге - Кутта уравнения ( 45) при данных граничных условиях были вычислены значения функций УО (), l i ( i) и УЗ () по значениям Р, принятым в расчетах. С помощью найденного представления этих функций могут быть вычислены распределения температур в потоке разреженного газа по заданным температурам стенки. Поддержание неравномерно заданных температур стенки в условиях стационарного теплообмена ее с обтекающим газом должно осуществляться соответствующим подогревом стенки тепловыми источниками. Мощность этих источников может быть вычислена по температурному полю газа. Таким же путем могут быть вычислены коэффициенты теплообмена, необходимые для практических расчетов, но в этом случае нужно произвести еще один пересчет. Для физической интерпретации решения необходимо установить соответствие между переменными Блазиуса и физическими координатами х та у. Такое соответствие должно устанавливаться формулой - ( 32), разрешаемой относительно координаты у обтекающего стенку разреженного газа. [9]
На практике результаты численного интегрирования не точны из-за погрешности измерений и неточностей самого измерения, поэтому для улучшения точности определения k используется метод наименьших квадратов. [10]
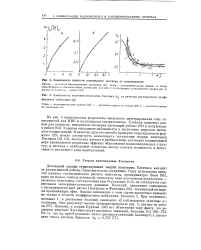 |
Зависимость вязкости полимерного раствора от концентрации.| Зависимость величины константы Хаггинса & н от качества растворителя ( коэффициента набухания оф. [11] |
На рис. 4 представлены результаты численного интегрирования этих зависимостей для ПВБ и полистирола соответственно. Хорошее совпадение наблюдается в достаточно широком интервале концентраций. В качестве другого способа проверки справедливости формулы ( 25) можно рассмотреть возможность построения теории константы Хаггинса [58, 64], поскольку именно в разбавленных растворах в наименьшей мере проявляются вторичные эффекты образования надмолекулярных структур, и поэтому с наибольшей точностью можно оценить истинность и допустимость различного рода приближений. [12]
В работе [10] приводятся результаты численного интегрирования системы уравнений, описывающих нестационарную фильтрацию жидкости и газа в неоднородной по кол-лекторским свойствам пористой среде с учетом сил гравитации. [13]
С этой целью используют результаты численного интегрирования дифференциального уравнения Лапласа ( см. с. [14]
Математические эксперименты выполняются в результате численного интегрирования дифференциальных уравнений конвективной диффузии в трещиновато-пористых средах при различных исходных данных и тех или иных начальных и граничных условиях. [15]
Страницы: 1 2 3 4