Результат - численное интегрирование - уравнение
Cтраница 1
Результаты численного интегрирования уравнения ( 3 - 7) хорошо согласуются с данными аналитического решения уравнений ( 3 - 23) и ( 3 - 25) в соответствующих условиях. [1]
Линии тока получаются в результате численного интегрирования уравнения (2.1) с и и v из (2.2) при произвольном выборе начальной точки в плоскости автомодельных переменных. Применительно к трехмерному стационарному обтеканию конуса под углом атаки они дают картину пересечений конических поверхностей тока с произвольной ( в силу автомодельности решения) плоскостью, перпендикулярной оси конуса. Как видно из рассчитанных описанным выше способом линий тока, изображенных на рис. 5, вихрь, привязанный через его уравнение движения к правой точке схода Si, находится в левой полуплоскости ( координата ( j отрицательна), а привязанный1 левой точке S - в правой. Это, однако, не соответствует исходной постановке задачи. Действительно, линия тока, которая является следом вихревой пелены, сходящей с точки Si, наматывается не на левый, а на правый вихрь. Линия тока, выходящая из точки S2, уходит на бесконечность и не связана ни с каким вихрем. [2]
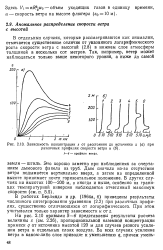 |
Зависимость концентрации s от расстояния до источника х ( а при различных профилях скорости ветра и ( б. [3] |
В работах Берлянда и др. ( 1964а, б) приведены результаты численного интегрирования уравнения (2.2) при различных профилях, существенно отличающихся от логарифмического. [4]
 |
Равновесные формы осесимметричных поверхностей раздела фаз ( максимальные участки устойчивости для задач типа I. [5] |
Строгое количественное определение физически реальных участков поверхностей раздела, полученных в результате численного интегрирования уравнения гидростатического равновесия ( задача (2.21), (2.22)), требует исследования устойчивости этих поверхностей к исчезающе малым возмущениям. В результате были выделены максимальные участки устойчивости интегральных кривых, которые приводятся на рис. 2.29 и 2.32 для случаев соответственно положительных и отрицательных перегрузок. [6]
Необходимо указать также недавнюю работу Кейна и Левинсо-на [22], в которой приводятся результаты численного интегрирования уравнений движения сферического волчка при той же гипотезе о кулоновом характере трения. [7]
Для полностью открытого всасывающего клапана справедливы все графические зависимости к f ( M, а), построенные в результате численного интегрирования уравнения ( 1) при постоянном критерии скорости потока [ 5, гл. [8]
Индекс т указывает на то, что значение данной величины берется в точке максимума. Результаты численного интегрирования уравнений ( 111 267) и ( 111 268) для большого числа различных параметров приведены в цитированной работе Баркелью в виде многочисленных графиков. [9]
Он исполь-эвал результаты численного интегрирования уравнений ( VI 21) гобы построить схемы, изображающие области значений параметров ри которых существует опасность высокой чувствительности Его езультаты обобщены в серии графиков, образец которых воспроиз-еден в принятых нами обозначениях на рис. VI-8. Три сплошных инии показывают влияние порядка реакции при условии, что темпе-атура подаваемой в реактор смеси равна температуре хладагента. [10]
 |
Корреляций параметрической чувствительности Баркелью ( 1959 г. ]. [11] |
Он использовал результаты численного интегрирования уравнений ( VI, 21), чтобы построить схемы, изображающие области значений параметров, при которых существует опасность высокой чувствительности. Его результаты обобщены в серии графиков, образец которых воспроизведен в принятых нами обозначениях на рис. VI-8. Три сплошных линии показывают влияние порядка реакции при условии, что температура подаваемой в реактор смеси равна температуре хладагента. [12]
При, отличном от нуля, производительность по фильтрату вследствие уменьшения расхода суспензии с течением времени также уменьшается. Графики функции V - f ( r) ( рис. 3 - 1), построенные по данным, полученным в результате численного интегрирования уравнения (3.15) с помощью ЭВМ, отклоняются от линейной зависимости и не имеют асимптот. Эти графики имеют точки перегиба, однако найти их аналитическим путем не представляется возможным. [13]
Функции VQ H V0 имеют быстро затухающий характер и оказывают влияние только на концах интервала. Малость параметра в позволяет вести инженерные расчеты с высокой степенью точности по первому приближению, не прибегая ко второму. Справедливость этого подтверждают результаты численного интегрирования уравнения ( 40) на ЭВМ. [14]
Видно, что т энергично возрастает в области действия градиента давления, а затем сравнительно медленно приближается к предельному значению, равному т 12 и 8.6 для двух рассмотренных случаев. Используя зависимость 0 ( U) из работы [27] и предполагая, что в области действия градиента давления толщина следа Ъи - ( С /) 1, получим r ( U / Uo) 4 17.6. Другой возможной гипотезой для вычисления т может служить предположение о постоянстве турбулентной вязкости вдоль следа е - const, в этом случае получим, что т ( U / Uo) 2 4.2. Кривые 5 и б на рис. 7 приближенно описывают поведение т в соответствии с этими гипотезами. Видно, что экспериментальные данные лучше согласуются с результатами численного интегрирования уравнений движения и вязкости. [15]
Страницы: 1 2