Дискретный аналог

Cтраница 1

Дискретные аналоги в виде (2.42) для внутренних расчетных точек и в виде (2.53) для граничных расчетных точек могут быть одновременно решены как система алгебраических уравнений. [1]

Дискретный аналог соотношений (1.2.4) - (1.2.8) записывается просто. [2]

Дискретный аналог функции Ф ( л: , у) - матрица отсчетов Ф у содержит множество значений сигнала при л обом положении растра в поле анализа, если движение растра плоскопар шлельное или чисто вращательное. Выборка этих значений по закону x ( t) y ( t) позволяет получить матрицу-столбец значений временного сигнала на выходе анализатора изображения. [3]

Дискретный аналог пункта ( б) теоремы транзитивности для сферы в общем случае не имеет места. Эти соотношения справедливы лишь в отдельных частных случаях. [4]

Дискретный аналог соотношений (1.2.4) - (1.2.8) записывается просто. [5]

Дискретный аналог исходной задачи при применении MKd oO - разует совокупность уравнений, описывающих деформативные свойства каждого элемента, уравнения совместности деформации соседних элементов и уравнения, являющиеся следствием уравнений равновесия в вариационной форме. [6]

Дискретные аналоги уравнений движения (5.44) и энергии (5.45) строятся по явной схеме, конечно-разностная аппроксимация уравнения Пуассона для обеспечения устойчивости - по неявной. Явные схемы позволяют по значению искомых функций на и-м временном шаге определять их значения на л 1 - м шаге. Решение уравнения Пуассона ведется методом прогонки. [7]

Дискретный аналог дифференциальных уравнений представляет собой алгебраические уравнения, связывающие значение Ф в некоторой группе узловых точек. Эти уравнения получаются из дифференциальных уравнений, описывающих изменение Ф, и, следовательно, этот аналог несет ту же физическую информацию, что и исходные дифференциальные уравнения, В дискретный аналог входят значения Ф только в некоторых узловых точках, что является следствием кусочного характера выбранных профилей. При этом значение Ф в некоторой узловой точке оказывает влияние только на распределение Ф в окрестностях этой точки. Предполагается, что при очень большом числе узлов решение дискретного аналога сближается с точным решением соответствуюшего дифференциального уравнения. Возможные дискретные аналоги любого дифференциального уравнения не единственны, однако, предполагается, что в пределе очень большого числа узловых точек все типы дискретных аналогов дают одно то же решение. Возможные отличия в решениях являются следствием различных предположений о характере профиля зависимой переменной и способов получения аналогов. [8]

Дискретным аналогом этого процесса может служить следующая модель случайного блуждания. Дх-0, получается непрерывное случайное блуждание, характерное для физического процесса броуновского движения. [9]

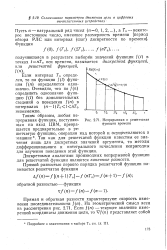Непрерывная и решетчатая функции времени. [10]

Дискретными аналогами производных непрерывной функции для решетчатой функции являются конечные разности. [11]

Дискретным аналогом этого процесса может служить следующая модель случайного блуждания. Ддг - - 0, получается непрерывное случайное блуждание, характерное для физического процесса броуновского движения. [12]

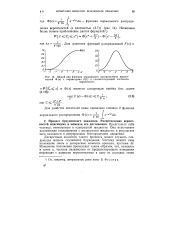Общий вид функции нормального распределения вероятностей Ф ( х с параметрами ( 0 1 и соответствующей плотности. [13]

Дискретным аналогом такого процесса может служить следующая модель случайного блуждания. [14]

Найден дискретный аналог уравнений Ламе и доказано, что эти уравнения являются необходимыми и достаточными для того, чтобы его решения являлись с точностью до калибровочного преобразования коэффициентами вращения решетки Дарбу-Егорова. Предъявлена схема построения явных решений дискретных уравнений Ламе в терминах тэта-функций Римана. [15]

Страницы: 1 2 3 4