Дискретный аналог

Cтраница 3

На второй стадии строятся дискретные аналоги дифференциального уравнения ( 1) и входных данных. [31]

При этом приходится решать дискретный аналог уравнения Фредгольма первого рода с разностным ядром. [32]

Существуют две основные версии дискретных аналогов: конечно-разностный метод и метод конечных элементов. [33]

Известно несколько способов построения дискретных аналогов ( разностной аппроксимации) производных. Наиболее распространенный способ основан на использовании метода разложения функций в ряд Тейлора. [34]

Распространим ее на случай обобщенного дискретного аналога. [35]

Сила для алгоритма с сохранением энергии, использующего линейное взвешивание заряда, кусочно-постоянна. [36]

Электрический потенциал является решением дискретного аналога уравнения Пуассона и представляет собой линейную комбинацию PJ и граничных условий, если последние неоднородны. [37]

Полудискретный аналог непрерывной области фильтрации.| Деление отрезка на равные интервалы. [38]

Известно несколько способов построения дискретных аналогов разностной аппроксимации) производных. Наиболее распространенный способ основан на использовании метода разложения функций в ряд Тейлора. [39]

Сложнее вопрос о построении дискретных аналогов граничных условий, в состав которых входят производные. [40]

Настоящая задача решается также дискретным аналогом градиентных схем, изложенным выше. [41]

В § 2.4 были построены дискретные аналоги как линейные алгебраические уравнения, которые были решены по алгоритму, разработанному для линейных уравнений. Однако в задачах теплопроводности довольно часто встречаются нелинейности. Граничные условия также могут быть нелинейными. Тогда дискретные аналоги уже не являются действительно линейными алгебраическими уравнениями. [42]

Для решения задачи расписания используется дискретный аналог градиентных схем для связанного экстремума. [43]

Воздействие дискретного оператора на случайную последовательность X ( t. а - образующая весовая функция. б-весовая функция дискретного оператора. в - дискретная последовательность х ( t. г - формирование ординат частной реализации выходного процесса у ( t. Знаком х обозначена последовательность (. [44]

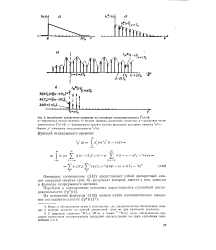
Очевидно, соотношение (3.42) представляет собой дискретный аналог операции свертки ( рис. 6), результат которой, вместе с тем, записан в функции непрерывного времени. [45]

Страницы: 1 2 3 4