Максимальное значение - критерий - оптимальность
Cтраница 1
Максимальное значение критерия оптимальности при этом достигается также на границе многогранника условий в л-мерном пространстве и может соответствовать как вершине этого многогранника, так и его граням, образованным различными пересечениями гиперплоскостей, составляющих этот многогранник. [1]
Максимальное значение критерия оптимальности ( Ф 1 6) получается при температуре 250 С, давлении 10 ат и условном времени контакта 0 5 час. [2]
 |
Пример задачи с незамкнутой областью изменения переменных и ограниченным значением критерия оптимальности. [3] |
Максимальное значение критерия оптимальности при этом достигается также на границе многогранника условий в n - мерном пространстве и может соответствовать как вершине этого многогранника, так и его граням, образованным различными пересечениями гиперплоскостей, составляющих этот многогранник. [4]
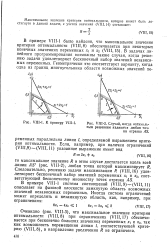 |
К примеру VIII-1.| Случай, когда оптимальным решением являются любая точка отрезка AS. [5] |
Очевидно ( рис. VIII-3), что максимальное значение критерия оптимальности ( VIII, 8) при ограничениях ( VIII, 17) обеспечивается при бесконечно больших значениях переменных х и х2, так как возможность перемещения линии /, соответствующей критерию ( VIII8), в направлении увеличения R не ограничена. [6]
Все найденные маргинальные значения положительны, следовательно, максимальное значение критерия оптимальности ( VIII, 231а), определяемое выражением ( VIII273), достигнуто. [7]
Однако это еще не означает, что уже достигнуто максимальное значение критерия оптимальности ( VIII, 85) и процесс поиска новых базисных решений, увеличивающих значение R, следует прекратить. [8]
Очевидно ( рис. VII1 - 3), что максимальное значение критерия оптимальности ( VIII8) при ограничениях ( VII 1 17) обеспечивается при бесконечно больших значениях переменных х1 и xz, так как возможность перемещения линии /, соответствующей критерию ( VIII8), в направлении увеличения R не ограничена. [9]
Однако это еще не означает, что уже достигнуто максимальное значение критерия оптимальности ( VIII85) и процесс поиска новых базисных решений, увеличивающих значение R, следует прекратить. [10]
 |
Пример задачи с незамкнутой областью изменения переменных и ограниченным значением критерия оптимальности. [11] |
Разумеется, при наличии незамкнутой области возможен также вариант, когда максимальное значение критерия оптимальности достигается при бесконечно больших значениях некоторых переменных. [12]
Задача оптимального проектирования реактора определенного типа сводится, таким образом, к разысканию максимального значения критерия оптимальности путем варьирования ряда независимых переменных, допустимые значения которых обычно ограничены технологическими пределами. Проведение процесса в рассчитанном режиме даст наилучший результат, достижимый ( в реакторе данного типа) на данном катализаторе при принятых условиях и ограничениях. Сравнивая максимальные значения критерия оптимальности для реакторов различных типов, можно определить, какой тип реактора предпочтителен для осуществления данного процесса. [13]
Задача оптимального проектирования реактора определенного типа сводится, таким образом, к разысканию максимального значения критерия оптимальности путем варьирования Ф независимых переменных, допустимые значения которых обычно ограничены технологическими пределами. [14]
Блок 2 засылает нулевые значения в массив [ fjv-f i ], в котором размещаются максимальные значения критерия оптимальности оптимизируемой стадии. [15]
Страницы: 1 2 3