Динамика - оболочка
Cтраница 2
В случае определения поведения жидкости конечно-разностными методами удобно применять эти же методы и для исследования динамики оболочки, что вызвано необходимостью стыковки на каждом шаге по времени решений уравнений движения жидкости и оболочки. Конечно-разностные методы являются также более экономичными по сравнению с методом Рунге-Кутты и, несмотря на то, что имеют меньший порядок аппроксимации по времени, не приводят к существенной потере точности. [16]
Далее, полагая массы сосредоточенными в узловых точках и следуя общей схеме ДВМ, получим дискретную модель динамики произвольных оболочек на основе трехмерных восьми - или шестиузловых элементов. [17]
В разделе описано несколько вариантов метода КИР для численного решения квазилинейных гиперболических систем уравнений, которые описывают динамику тонких деформируемых оболочек. [18]
U N по базису j можно установить взаимно однозначное соответствие, из чего вытекает эквивалентность второго варианта уравнений динамики оболочки ( краевая задача в коэффициентах) уравнениям проекционного метода. Таким образом, уравнения проекционного метода могут содержать в качестве неизвестных коэффициенты или моменты, приводить же граничные условия на боковых поверхностях оболочки к однородным с помощью замены Ut / W не обязательно. [19]
Однако найти структуру стационарной ударной волны в рассматриваемой среде не удается без использования всей информации, содержащейся в решении задачи о динамике паровой оболочки около находящейся в жидкости нагретой частицы. В этом заключается отличие используемых в настоящей работе макроскопического и микроскопического описаний движения. При микроскопическом описании учитываются нестационарные процессы динамического взаимодействия и тепло - и массообмена около отдельного включения. В результате увеличивается размерность задачи об одномерном движении дисперсной смеси. [20]
Различные варианты уравнений динамики оболочек приведены в гл. [21]
Различные варианты уравнений динамики оболочек приведены в гл. [22]
Таким образом, выше было представлено общее описание явного, условно устойчивого варианта метода расщепления для численного решения уравнений динамики тонких оболочек. Он основан на сведении уравнений динамики оболочек к квазилинейной гиперболической системе уравнений первого порядка и точном выделении быстро осциллирующих компонент решения. Метод позволяет также определять пределы применимости других методов, а также причины потери ими устойчивости. [23]
В актуальности своих научных разработок М.А.Ильгамов смог, например, убедиться во время поездки в Чехословакию, где побывал в институтах Академии наук этой страны в Праге и Братиславе. Оказалось, что чехословацкие специалисты с успехом применили результаты, изложенные в указанной выше монографии по динамике оболочек с жидкостью и газом, при расчете и проектировании трубопроводов большого диаметра для строящейся атомной электростанции. [24]
Это избавляет при численном решении от громоздких вычислений ковариантных производных в криволинейных базисах локальных координат, которые традиционно используются в теориях оболочек. Для моделей в точности выполняется закон сохранения механической энергии или теорема живых сил. В линеаризованном варианте волновые свойства полученных уравнений динамики оболочек сходны по скоростям распространения с линейной моделью трехмерного тела. Приведены эквивалентные вариационные формулировки нелинейных уравнений движения и виды естественных краевых условий, соответствующих принятым гипотезам. Они удобны для численности решения задач на основе МКЭ, ВРМ или ДВМ. [25]
Задача (7.3.12) - краевая задача неклассической теории оболочек, и ее интегрирование требует применения экономичных и эффективных численных методов, учитывающих существенные особенности таких задач - матричную структуру решения и сильную численную неустойчивость неклассических дифференциальных уравнений слоистых оболочек. Этим требованиям в полной мере отвечает разработанный в предыдущем разделе метод инвариантного погружения в его обобщенной форме. Накопленный вычислительный опыт [17-19, 21, 23, 24, 30] позволяет рекомендовать эту модификацию метода к широкому использованию в задачах прочности, устойчивости, динамики оболочек. [26]
В отличие от КАИ и нас, применяются более точные способы замеров, в том числе турбулентности. Имеются термоанемометры фирмы DISA, но много к ним своих приспособлений. Они здесь удивлялись, что я интересуюсь таким широким кругом вопросов: и теория оболочек, устойчивость и динамика оболочек, численные методы и эксперименты; и все то же по гидро - и аэродинамике. [27]
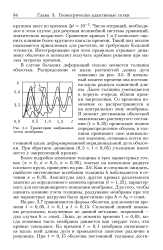 |
Траектории выбранных точек мембраны. [28] |
Число итераций, необходимое в этом случае для решения нелинейной системы уравнений, значительно возрастает. Сравнение кривых 1 и 2 позволяет оценить влияние более крупного шага по времени. Такой шаг вполне оказывается приемлемым для расчетов, не требующих большой точности. Интегрирование при этом правильно отражает динамику оболочки и позволяет получать пробные решения при малых затратах времени. [29]
Первое из них базируется на строгом учете структуры материала, второе - на использовании интегральных диаграмм деформирования, которые могут быть получены экспериментально или расчетным путем. В связи с этим при разработке методов решения задач статики и динамики оболочек из КМ структурные особенности последних учитываются только при расчете эффективных характеристик анизотропной сплошной среды, имеющей такие же диаграммы деформирования и прочностные характеристики, что и исходный КМ. Построив в таком приближении уравнения состояния КМ, а также используя уравнения движения и соотношения между перемещениями и деформациями теории упругости анизотропного тела, можно получить решение соответствующих задач, хотя это сопряжено со значительными трудностями. [30]
Страницы: 1 2