Критическое значение - нагрузка
Cтраница 3
Уравнение ( 23) дает возможность получить критическое значение нагрузки 72, при которой возможна потеря устойчивости в плоскости кольца. [31]
Используя ряд ( 1), выразим критическое значение нагрузки из уравнения ( 3) и исследуя это выражение на экстремум так подберем коэффициенты. [32]
Из условий закрепления получаем уравнение для определения критического значения нагрузки. [33]
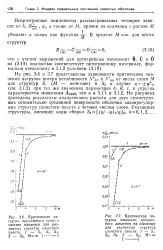
На рис. 3.6 и 3.7 представлены зависимости критических значений нагрузок потери устойчивости N xx и N yy от числа слоев М для структур 5 ] ( М - нечетное) и 52 в случае ср ср оо ( см. 3.1.2) при тех же значениях параметров h, R, L и упругих характеристик монослоев Лартб, что и в 3.1.1 и 3.1.2. На рисунках приведены результаты аналогичного расчета для двух симметричных относительно срединной поверхности оболочки квазирегулярных структур слоистого пакета с четным числом слоев. [35]
В теории устойчивости упругих пластин характерным является одно критическое значение нагрузки / к, при превышении которого начальное состояние идеально правильной пластины перестает быть устойчивым. В теории устойчивости тонких упругих оболочек выделяют два характерных значения нагрузки: Рк - критическая нагрузка, после достижения которой перестает быть устойчивым начальное напряженно-деформированное состояние идеально правильной оболочки; Р ц - нагрузка, при достижении которой происходит хлопок реальной оболочки с геометрическими несовершенствами формы. [36]
С помощью линеаризованных уравнений и энергетического критерия определяют критические значения нагрузок и те формы, по которым происходит потеря устойчивости. [37]
Первые два из выражений ( 46) представляют собой критические значения нагрузки, соответствующие изгибным или эйлеровым формам равновесия, и третье выражение дает критическую нагрузку, связанную с крутильной формой равновесия. Таким образом, вычисление критических нагрузок для тонкостенных открытых профилей по формулам Эйлера возможно, вообще говоря, только в том частном случае, когда продольная сжимающая сила приложена в центре изгиба сечения. Если же точка приложения продольной силы не совпадает с центром изгиба, то стержень обладает только из-гибно-крутильными формами равновесия. Некоторое исключение из этого общего положения представляют сечения с одной или двумя осями симметрии при условии, что точка приложения продольной силы лежит на оси симметрии. [38]
Наличие промежуточных опор весьма существенно отражается на величине критического значения нагрузки. [39]
При практическом применении изложенного выше точного метода вычисления критического значения нагрузки на пластину в ряде случаев возникают значительные трудности в нахождении решения дифференциального уравнения срединной поверхности, удовлетворяющей заданным краевым условиям. Кроме того, трансцендентность уравнений, к которым приводит точный метод, не позволяет выразить критическую нагрузку в явной форме. Поэтому, так же как и при рассмотрении устойчивости сжатых стержней, наряду с точным методом целесообразно использование приближенного метода расчета, основанного на рассмотрении потенциальной энергии выпучившейся пластины. [40]
Наличие промежуточных опор весьма существенно отражается на величине критического значения нагрузки. [41]
В монографиях [28] и [29] приведены таблицы коэффициентов критического значения нагрузки для трехступенчатых симметричных стоек как с опертыми, так и с заделанными концами, нагруженных торцовыми силами. [42]
Возникает задача об, оценке устойчивости системы по известным критическим значениям нагрузок, отвечающих каждому воздействию в отдельности. [43]
Это уравнение вместе с соответствующими краевыми условиями позволяет определить критическое значение нагрузок Р и Т ( фиг. [44]
При отсутствии табличных данных необходимо обращаться к непосредственному вычислению критического значения нагрузки. [45]
Страницы: 1 2 3 4