Подходящее значение - параметр
Cтраница 1
Подходящие значения параметров можно искать графически, как рекомендовано в [85], или с помощью метода максимума правдоподобия, рассматривая K ( Klt K2) в качестве параметра ( параметров) распределения и записывая функцию правдоподобия для исходных переменных. [1]
Чаще всего для выбора подходящего значения параметра сглаживания используют способ невязки. [2]
Для нахождения асимптотики чисел an R нужно выбрать подходящее значение параметра х, подставить его в выражение для распределения (4.3.2) и доказать локальную теоремы для суммы независимых слагаемых с этим распределением. [3]
В этих задачах интуитивно ясно, что при подходящих значениях параметров Е окажется способным пройти мимо Р и избежать захвата из всех ( за исключением, может быть, некоторого несущественного множества) начальных точек. [4]
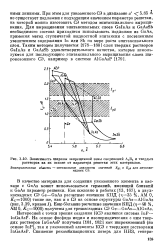 |
Зависимость ширины запрещенной зоны соединений А3В5 и твердых растворов на их основе от параметра решетки этих материалов. [5] |
При этом для узкозонного СЭ в диапазоне a f 5.85 А не существует подложки с подходящим значением параметра решетки, на которой можно изготовить СЭ методом эпитаксиального выращивания. Для выращивания эпитаксиальных слоев GalnAs и GaAsSb необходимого состава приходится использовать подложки из GaAs, применяя метод ступенчатой жидкостной эпитаксии с постепенным увеличением содержания In или Sb по мере роста эпитаксиального слоя. [6]
Затем, подгоняя ее под эмпирическое распределение величин vesmi для данной группы звезд, мы определяем подходящие значения параметров. [7]
Выражение, стоящее под знаком логарифма в данном неравенстве, всегда больше единицы, и поэтому при всяком подходящем значении параметра t должно выполняться неравенство. [8]
Франк-Каменецкий [10] показал даже, что взрывы H2S и N20 и С2Н2 [11] тоже могут быть описаны такими уравнениями и, используя подходящие значения параметров, можно вычислить значения В в хорошем соответствии с опытом. [9]
Франк-Каменецкий [10] показал даже, что взрывы H2S и N20 и С2Н2 [11] тоже могут быть описаны такими уравнениями и, используя подходящие значения параметров, можно вычислить значения Б в хорошем соответствии с опытом. [10]
Ел Eg - ( 1 3m / и2) эВ, где Eg - ширина запрещенной зоны, т - эффективная масса электронно-дырочной пары, выраженная в единицах электронной массы, Еп - энергия возбужденного светом СТ-экситона, п - целое положительное число. Выбирая подходящие значения параметров, можно получить энергии СТ-экситонов, указанные в табл. 2.7, и вычислить величины разности Eg - En Ea. Зависимость рассчитанных таким образом значений энергии активации разделения зарядов от энергии возбуждающих квантов ( или Еп) представлена на рис. 3.2.14; там же для сравнения приведены и значения, измеренные Като и Брауном. Учитывая, что Баундс и Зибранд для получения хорошо согласующихся с экспериментом конечных результатов сделали много довольно серьезных допущений, необходима дальнейшая работа, которая окончательно доказала бы справедливость этих выводов. [11]
Замечание 12.5. Все используемые в представленной выше схеме прогнозирования параметры ( т, N, L) следует определять на этапе обучения схемы прогнозирования с использованием реализованной части исследуемого временного ряда. Критерием отбора подходящих значений параметров в процессе обучения прогнозируемой схемы должно являться качество прогноза, например сумма квадратов невязок между прогнозируемыми и реализованными значениями исследуемого временного ряда. [12]
Заметим, что в рамках байесовского подхода при неизвестных параметрах законов распределения эти параметры должны рассматриваться как случайные величины и необходимо задавать априорную плотность вероятности этих случайных величин. В частности, определение подходящего значения параметра регуляризации в рамках байесовского подхода невозможно, если не задавать априорное распределение возможных значений этого параметра. [13]
Изменение значения любой переменной, коррекция любой формулы означает, что все расчеты, зависящие от этой величины, необходимо проделать заново. Такая необходимость возникает при выборе подходящих значений параметров или условий, поиске оптимального варианта, исследовании зависимости результата от начальных условий. Электронный документ, подготовленный в программе MathCad, готов к подобной ситуации. При изменении какой-либо формулы программа автоматически производит необходимые вычисления, обновляя изменившиеся значения и графики. [14]
При этом учитывают возможность постановки не реализуемых по разным причинам на самом объекте исследования спец. Задача идентификации модели обычно сводится к задаче минимизации критерия адекватности объекту путем подбора подходящих значений уточняемых параметров и вида вызывающих сомнение зависимостей. [15]
Страницы: 1 2