Парциальное значение
Cтраница 2
Выше было показано, что изотермические изменения летучести и парциальных значений энтальпии, энтропии и внутренней энергии для компонентов смеси можно оценивать с помощью констант уравнения состояния. Для иллюстрации этого было использовано уравнение БВР. Так же могут применяться и другие уравнения состояния. Следует отметить, что уравнение состояния не обеспечивает достаточной информации для оценки неизотермического изменения термодинамических ( характеристических) функций. [16]
Из величин ДО0, ДЯ и Д5 могут быть вычислены парциальные значения соответствующих функций для растворенного кислорода. [17]
H, S или F) Это выражение означает, что парциальное значение свойства G для k - то компонента в данной фазе, находящейся в определенном состоянии, равно скорости изменения общего значения G для фазы в целом при добавлении бесконечно малого количества компонента k и условии, что температура, давление и вес остальных компонентов остаются постоянными, характерными для данного состояния. [18]
Аналогично с помощью таких же производных и при тех же условиях определяются молярные парциальные значения других экстенсивных величин. [19]
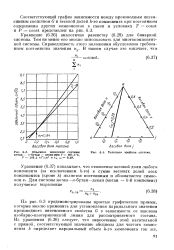 |
Объемное поведение системы. [20] |
На рис. 6.3 продемонстрированы простые графические приемы, которые можно применить для установления парциального значения производного интенсивного свойства G в зависимости от наклона изобарно-изотермической линии для рассматриваемого состава. [21]
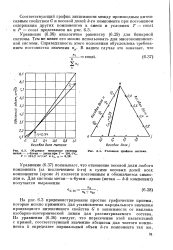 |
Объемное поведение системы.| Условная тройная система. [22] |
На рис. 6.3 продемонстрированы простые графические приемы, которые можно применить для установления парциального значения производного интенсивного свойства G в зависимости от наклона изобарно-изотермической линии для рассматриваемого состава. [23]
Для решения проблемы расчета свойств стекла по составу нет нужды проводить различия между формальными и собственными парциальными значениями свойств компонентов в стекле, но это необходимо делать, если мы хотим, на основании исследования парциальных свойств компонентов, высказывать какие-либо суждения об их структурном состоянии. Существенными характеристиками химической природы и структурного состояния - компонентов могут быть лишь те величины gi, которые близки к собственным парциальным свойствам компонентов. [24]
Заметим, что химический потенциал щ данного компонента I в какой-нибудь смешанной фазе равен парциальному значению энергии Гиббса G, этого компонентам данной фазе. [25]
Если сопутствующие параметры не связаны стохастически с ведущим параметром, то их расчетные значения просто совпадают с наиболее вероятными парциальными значениями. [26]
Если Т и р в системе остаются постоянными, то химический потенциал ц данного компонента i в какой-нибудь смеси равен парциальному значению изобарного потенциала Z этого компонента в данной фазе. В простых фазах величине химического потенциала соответствует просто изобарный потенциал данного вещества. [27]
Если Т и р в системе остаются постоянными, то химический потенциал цг данного компонента i в какой-нибудь смеси равен парциальному значению изобарного потенциала Z этого компонента в данной фазе. В простых фазах величине химического потенциала соответствует просто изобарный потенциал данного вещества. [28]
РМ - рассматриваемое свойство молекулы; рэ - парциальные значения свойства Р, сопоставляемые отдельным эффективным атомам; р ( э э) - парциальные значения свойства Р, сопоставляемые отдельным парам эффективных атомов в молекуле. [29]
Последнее уравнение характеризует изменение концентрации dxi, о растворенного вещества с изменением давления дР при постоянной температуре как функцию отношения разности молярных объемов в обеих фазах к градиенту изменения парциального значения энергии Гиббса. [30]
Страницы: 1 2 3 4