Среднее значение - квадрат
Cтраница 1
Среднее значение квадратов и 2 колебаний, как среднее только положительных значений, всегда больше нуля, среднее же произведений u v может быть как положительным, так и отрицательным, а также равным нулю. [1]
Среднее значение квадрата синуса и квадрата косинуса равно, как известно, половине. [2]
Среднее значение квадрата косинуса равно половине. [3]
Среднее значение квадрата момента, как и в классической механике, равно сумме средних значений квадратов проекций. [4]
Среднее значение квадрата смещения броуновской частицы за промежуток времени Д / вдоль оси X, или любой другой оси, пропорционально этому промежутку времени. [5]
Среднее значение квадратов расстояний элементов массы до данной оси называют квадратом плеча или радиусом инерции тела. [6]
Среднее значение квадрата смещения броуновской частицы за промежуток времени Ы вдоль оси X, или любой другой оси, пропорционально этому промежутку времени. [7]
Вычислим среднее значение квадрата функции, стоящей в скобках, при этом приведенный момент инерции будет постоянным. [8]
Вычислим среднее значение квадрата относительной флюктуации б2 числа частиц, появляющихся в поле зрения микроскопа в рассмотренном нами опыте Сведберга. [9]
Выразим среднее значение квадрата напряженности поля через излучаемую антенной мощность. [10]
Найти среднее значение квадрата расстояния точки круга ( х-а) 2 ( у - Ь 2 К2 от начала координат. [11]
Аналогично определяется среднее значение квадрата случайной величины. [12]
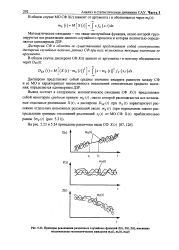 |
Примеры реализации различных случайных функций X ( t, Y ( f, Z ( t, имеющих неодинаковые математические ожидания mx ( f, mtf, MZ (. [13] |
Дисперсия представляет собой среднее значение квадрата разности между СФ и ее МО и характеризует интенсивность отклонений относительно среднего значения; определяется одномерным ДЗР. [14]
Итак, среднее значение квадрата смещения броуновской частицы за промежуток времени t пропорционально этому промежутку. Соотношение (17.61) называется формулой Эйнштейна. [15]
Страницы: 1 2 3 4