Среднее значение - произведение
Cтраница 2
 |
Капиллярная модель зернистого слоя. [16] |
Скобками обозначено среднее значение произведения вдоль капилляра. Но поскольку слой в целом можно считать макроскопически однородной средой, то усреднение в (1.90) следует производить по всему объему. Среднее значение произведения, вообще говоря, не равно произведению средних значений его сомножителей, особенно, если они еще взаимозависимы, что наблюдается в данном случае. [17]
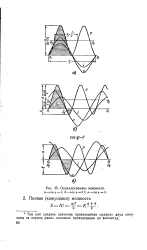 |
Осциллограммы мощности, а - cos р 1. б - cos у 0 7. в - cos р 0. [18] |
Так как среднее значение произведения ординат двух синусоид за период равно половине произведения их амплитуд. [19]
Как известно, среднее значение произведения, вообще говоря, не равно произведению средних значений его сомножителей, особенно, если они еще взаимозависимы, как это и - есть в данном случае. При одинаковой форме зависимости Ap / L от а и е, числовой коэффициент пропорциональности в этой зависимости может различаться для слоев из зерен различной конфигурации на 20 - 30 %, что, правда, может считаться удовлетворительным при конструировании расчетных инженерных формул. [20]
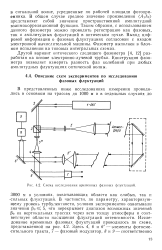 |
Схема исследования временных фазовых флуктуации. [21] |
В общем случае среднее значение произведения ( AiAz) представляет собой значение пространственной амплитудной взаимокорреляционной функции. [22]
Заметим, что среднее значение произведения пульсационных скоростей и их производных, вообще говоря, не равно нулю. [23]
Эта формула позволяет представить среднее значение произведения функционалов через произведение средних значений самих функционалов. [24]
Однако член, содержащий среднее значение произведения входных сигналов м () и2 (), появляется только за счет наличия квадратичного члена полинома. [25]
Корреляционная функция определяется как среднее значение произведения флуктуации дипольного момента в двух узлах решетки. [26]
При т Т0, рассматривая среднее значение произведения х ( t) x ( t т) на интервале Т0 для четырех возможных равновероятных вариантов, когда переключение происходит при / и i - ( рис. 9.9, о), t - и t 0 ( рис. 9.9, б), г0 и L. [27]
Отсюда же следует, что среднее значение произведения чисел частиц в двух элементах dt и iT2 совпадает с вероятностью одновременного нахождения в каждом из них по одной частице. Для заданной пары частиц это есть, по определению двухчастичной функции распределения, произведение / 8Ит та. [28]
Отсюда же следует, что среднее значение произведения чисел частиц в двух элементах dr и dr % совпадает с вероятностью одновременного нахождения в каждом из них по одной частице. [29]
Коэффициент корреляции представляет собой отношение среднего значения произведения двух переменных к квадратному корню из произведения их средних квадратов. [30]
Страницы: 1 2 3 4