Зом-мерфельда
Cтраница 1
Зом-мерфельда; k - постоянная Больцмана; а / ( /, ш) - 1 - коэффициент, определяемый из эксперимента, шо - частота, соответствующая красной границе. Соотношение ( 13) является приближенным; оно получено для модели, в которой предполагается, что все электроны имеют энергию Ферми, а те, которые могут преодолеть потенциальный барьер, не испытывают столкновений. Строгая теория [12] дает результаты, лучше согласующиеся с экспериментом для больших частот излучения. Однако приближенное соотношение ( 13) позволяет с удовлетворительной точностью описать выход электронов в области частот, не сильно превышающих красную границу. [1]
Из правила квантования Бора - Зом-мерфельда для куперовской пары, движущейся в сверхпроводнике, следует, что связанный с нею магнитный поток оказывается квантованным. [2]
Уравнение (7.2.7) известно как уравнение Орра - Зом-мерфельда. [3]
Уравнения (11.10.8) и (11.10.9) представляют собой обычные уравнения Орра - Зом-мерфельда для течения, развивающегося в условиях естественной конвекции около поверхности, нагреваемой равномерным тепловым потоком. [4]
У Планка никогда не было научной школы, как у Зом-мерфельда в Мюнхене, и число учеников, писавших под его руководством диссертации, невелико. [5]
Уравнения (11.10.8) и (11.10.9) представляют собой обычные уравнения Орра - Зом-мерфельда для течения, развивающегося в условиях естественной конвекции около поверхности, нагреваемой равномерным тепловым потоком. [6]
Отто Штерн и Вальтер Герлах экспериментальным путем доказывают правильность представлений Рождественского и Зом-мерфельда при объяснении сложности атомного спектра. [7]
Боровский метод квантования круговых электронных орбит является частным случаем метода квантования Вильсона - Зом-мерфельда. [8]
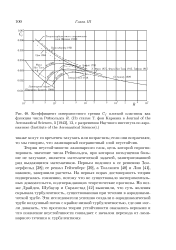
В применении к электронам справедливость статистики Ферми была вскоре подтверждена работами Паули и Зом-мерфельда о металлах. Эти электроны называются свободными. В грубом приближении можно себе представить, что внутри металла свободные электроны движутся совершенно свободно, так, как если бы на них не действовали никакие силы, и что последние появляются лишь в поверхностном слое металла. Так, например, согласно последней, свободные электроны должны были бы участвовать в тепловом движении наравне с атомами, и, следовательно, теплоемкость металлов должна была бы быть значительно больше, чем теплоемкость неметаллических одноатомных тел. В действительности теплоемкость тех и других, отнесенная к одному и тому же числу атомов, оказывается практически одинаковой по крайней мере в области не слишком высоких температур. Это обстоятельство непосредственно объясняется статистикой Паули-Ферми. Если мы взглянем на кривую 2 ( рис. 2), то увидим, что наклон ее к горизонтальной оси, определяющий теплоемкость, очень мал при 7 0 и приобретает нормальную ( классическую) величину лишь при более высокой температуре. [9]
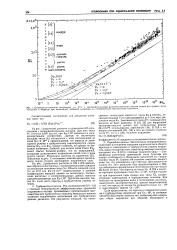
Теория неустойчивости ламинарного слоя, цель которой спрогнозировать значение числа Рейнольдса, при котором возмущения больше не затухают, является математической задачей, заинтриговавшей ряд выдающихся математиков. Первым подошел к ее решению Зом-мерфельд [38]; ее решал Гейзенберг [39], а Толлмиен [40] и Лин [41], наконец, завершили расчеты. [11]
Значительная неопределенность существует в отношении поведения характеристик в области перехода от ламинарного к турбулентному режиму конвекции, даже в отношении того, какие безразмерные комплексы описывают его. В [21] с помощью уравнения Орра - Зом-мерфельда рассчитаны критические числа Грасгофа для потери устойчивости и обнаружено увеличение их с возрастанием числа Рг. [13]
После того как дифференциальные уравнения движения написаны на основании вариационного принципа Гамильтона, возникает вопрос об их фактической интеграции. Для этой цели Гамильтоном и Якоби развита специальная теория. Эта теория имеет особое значение для небесной механики и для классической теории атома Бора - Зом-мерфельда. Построение этой теории должно было заключать в себе три последовательных этапа. Прежде всего необходимо было найти возможно более простую форму дифференциальных уравнений движения. Эта форма была найдена в канонических уравнениях Гамильтона. [14]
Если параметр в гамильтониане меняется настолько медленно, что в его фурье-разложений оказываются только частоты ниже определенного значения, скажем v0, которое меньше, чем любая частота, соответствующая боров-ским условиям для квантовых переходов, то га время изменения параметра никакие квантовые переходы происходить не могут. Это в свою очередь означает, что по мере медленного изменения параметров, происходящего в гамильтониане, не могут изменяться квантовые числа; тем более не могут изменяться квантованные величины. Поскольку переменные действия оказались адиабатическими инвариантами, они могут служить подходящими объектами для квантования; фактически именно для них были предложены правила квантования Вильсона - Зом-мерфельда. [15]
Страницы: 1 2