Зоммерфельд

Cтраница 2

Зоммерфельд в своем Электричестве вспоминает, vro Вейерштрасс нашел идеи Римана непонятными, тогда как более интуитивный Гельмгольц схватил их сразу. [16]

Зоммерфельдом было теоретически доказано [290], что прямой цилиндрический проводник с конечной проводимостью и гладкой поверхностью может служить направляющей системой для электромагнитных волн. Хармс [129] показал, что аналогичное распространение поверхностных волн имеет место и при бесконечной проводимости, если только поверхность металл а покрыта диэлектрическим слоем. На рис. 10.10 показаны геометрия направляющей системы и распределение поля основной волны. При бесконечном увеличении радиуса цилиндра эта продольная волна переходит в плоскую волну над плоской поверхностью. [17]

Зоммерфельдом и примерно в то же время было подтверждено экспериментально Пашеном возможно, оно было самым большим триумфом этой теории, вслед за объяснением Бора серии Бальмера и его вычислением числа Ридберга из универсальных атомных констант. Первоначальная формула Зоммерфельда была полностью восстановлена только с появлением рассмотренной здесь теории Дирака. Восстанавливается также квантовое число k, которое использовалось в старой квантовой теории вместо / и которое может принимать значение 0, но теперь оно снабжено еще и знаком. [18]

Зоммерфельдом [209]: если известен достаточно большой набор частных решений, то посредством интерполирования можно составить представление о свойствах вращения твердого тела в общем случае. Однако дальнейшее развитие теории динамических систем не подтвердило концепцию Клейна - Зоммерфельда. В фазовом пространстве задачи о вращении тяжелого твердого тела вокруг неподвижной точки почти всегда имеются зоны квазислучайного движения, наличие которых никак нельзя вывести из факта существования большого числа периодических или условно-периодических траекторий. [19]

Зоммерфельдом, Н. Е. Жуковским, С. А. Чаплыгиным и др. Основное положение теории гидродинамической смазки, при которой трущиеся поверхности полностью изолированы масляной пленкой, следующее. [20]

Зоммерфельдом было электронный газ в металле является вырожденным. Расчет кости по формулам квантовой статистики Ферми - Дирака дает результаты, согласующиеся с опытом, так что модель идеального электронного газа в металле подтверждается и в этом случае. [21]

Зоммерфельдом - Дебаем применительно к компрессору двойного действия. [22]

Работа Зоммерфельда, написанная им совместно с Клейном, была одной из первых работ этого автора по теории волчка, тогда как эта книга, опубликованная более чем 40 лет спустя, является одной из последних его работ. [23]

Эффект Зоммерфельда в системе со случайно изменяю щейся собственной частотой. [24]

Книга Зоммерфельда является хорошим введением в механику как отдел теоретической физики. Написанная с большим педагогическим мастерством, она, несмотря на небольшой объем, отличается богатством содержания. Много внимания автор уделяет выяснению физического смысла законов и понятий механики, чему способствует большое количество оригинальных физических примеров и задач. [25]

Теории Зоммерфельда и Уильсона страдали тем существенным недостатком, что не удавалось указать каких-либо правил для выбора координат, к которым должны быть приложены квантовые условия. Это очевидно только для специального случая кеплерова эллипса. [26]

Число Зоммерфельда, рассчитываемое на основе классической теориЕ гидродинамической смазки по формуле r V / P, является единственным безразмерным параметром, широко применяемым при конструировании опорных подшипников. В случае скольжения сферы число Зоммерфельда имеет вид [14]: iVK / P, npi этом влияние упругой деформации не учитывается. Согласно уравне нию (7.22) упругие эффекты учитываются параметром ( E / qo), которых можно рассматривать как упругое число. Произведение этого числ; на число Зоммерфельда [ см. формулу (7.22) ] называется эластогид родинамическим числом ЕН. Это число представляет собой расши ренное число Зоммерфельда, учитывающее упругие деформации одно. Хотя выражение ЕН было получено для случая малы:: нормальных сил, в действительности оно нашло широкое применение о чем будет сказано ниже. [27]

Теория Зоммерфельда, которую мы изложим в настоящей главе, пренебрегает учетом периодического хода электрического потенциала в решетке кристалла, считая потенциал постоянным во всем металле. [28]

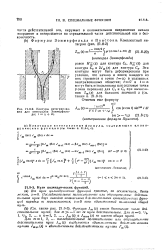Контуры интегрирования для интегралов Зоммерфельда. 1 - у ill. [29]

Формулы Зоммерфельда и Пуассона. [30]

Страницы: 1 2 3 4