Верхняя валентная зона

Cтраница 1

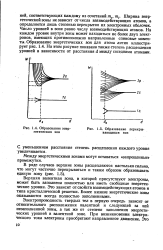Образование энергетических зон.| Образование перекрывающихся зон. [1]

Верхняя валентная зона, в которой присутствуют электроны, может быть заполнена полностью или иметь свободные энергетические уровни. Это зависит от свойств взаимодействующих атомов и типа кристаллической решетки. Более низкие энергетические зоны оказываются всегда полностью заполненными. [2]

Для верхней валентной зоны, образованной в основном р-функциями С1 -, результаты для двух наборов функций отличаются мало. Дно зоны проводимости, однако, при расчете с первым набором получается слишком низким по энергии, так как 45-функции К плохо передают это состояние. Включение в базис Ss-функций С1 - заметно улучшает результат, а в соответствующей МО оказывается довольно велик вес Зз-функций. Этот выход согласуется с данными расчетов И. В. Абаренкова для дна зоны проводимости в кристалле КС1 по методу модельного потенциала: максимум соответствующей волновой функции получается не в окрестности иона К, а практически посередине между ионами К. [3]

Данные для верхней валентной зоны. [4]

Положение дна верхней валентной зоны, к сожалению, трудно установить однозначно, поскольку различные экспериментальные оценки для ширины валентной зоны в кристалле КС. [5]

Данные для верхней валентной зоны. [6]

Результирующее изменение зон, проявляющееся в искривлении верхних валентных зон ( и изменении кривизны других зон) показано на третьем рис. 6.3. В рамках модели Vi-зон эти эффекты отсутствуют. При этом не меняется ни полная ширина зоны, ни величина щели в точке X. [7]

Электронная структура центра KC1 - TI в модели КРЭЯ ( энергия в эВ. [8]

В табл. 5.1 приведены энергии локальных уровней примесного катиона Т1, расположенных ниже верхней валентной зоны ( состояние Iflig) и в запрещенной зоне ( 2alg); приведены рассчитанный заряд на атоме Т1 ( 7тО Для всех рассмотренных ячеек и число базисных функций, использованных в расчетах соответствующих квазимолекул. [9]

Отнесение МО к определенным зонным состояниям произведено с учетом вырождения энергетических зон, входящих в верхнюю валентную зону. Благодаря применению симметризованного атомного базиса были рассчитаны очень большие квазимолекулы - Кб4С1в4 и KiosCliog, содержащие 128 и 216 атомов и полученные соответственно растяжением вчетверо векторов трансляции примитивной ячейки и втрое векторов трансляции кубической ячейки. Соответственно векторы k из 8 и 10 звезд в неприводимой части зоны Бриллюэна приводятся к центру суженной зоны. Заметим, что в кристалле КС1 скачок заряда при переходе от минимальной элементарной ячейки к расширенной заметно меньше, чем в LiH. [10]

Напротив, зоны с энергиями, большими EHQ, приводят к увеличению т или даже делают т отрицательной, как в случае верхних валентных зон в полупроводниках типа алмаза и цинковой обманки. [11]

Ширина зоны d ( определяется главным образом интегралом do - перекрытия. Верхняя валентная зона относительно плоская вследствие слабого перекрытия ррп - и доо-орбиталей. [12]

Пантелидес и Харрисон отмечали, что если положить V5 тождественно равным нулю и выразить V и V5 через атомные матричные элементы, то 1 / 4 оказывается в точности равным - Vppn. Этот интересный результат позволяет предположить, что кривизна верхних валентных зон должна определяться п-связью, антисвяЗывающими состояниями в точке Г и связывающими состояниями в точке X. Анализ самих состояний подтверждает этот вывод. Действительно, вычитая (6.5) из (6.2), убеждаемся в том, что в гомеополярных полупроводниках энергетический интервал между этими состояниями оказывается равным 4Уррл даже в том случае, когда не используется метод связывающих орбиталей. [13]

Одноосное напряжение, приложенное к образцам р-типа, снимает вырождение двух верхних валентных зон, и при высоких напряжениях зона легких дырок смещается вниз настолько, что оказывается не занятой при температурах жидкого гелия. Таким путем Хенселу [316] удалось исследовать циклотронный резонанс, связанный примерно с десятью различными переходами на лестницу уровней Ландау для тяжелых дырок ( разд. [14]

МО, образованные теми же атомными функциями, оказываются выше по энергии, чем р-состояния лития, модифицированные полем кристалла. В ЩГК s - функщш катионов слабо смешиваются с р-функциями анионов, которые образуют верхнюю валентную зону, и дно зоны проводимости в ЩГК оказывается s - типа. Расчеты показывают, что включение в базис р-функций аниона в кристалле LiF мало сказывается как на валентной зоне, так и на нижних по энергии состояниях зоны проводимости. [15]

Страницы: 1 2