Верхняя валентная зона

Cтраница 2

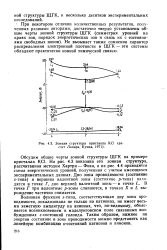Зонная структура кристалла КС1 ( расчет Линари, Кунца, 1971. [16]

На рис. 4.3 показана его зонная структура, рассчитанная методом Хартри - Фока, а на рис. 4.4 приводится схема энергетических уровней, полученная с учетом имеющихся экспериментальных данных. Дно зоны проводимости ( состояние s - типа) и вершина валентной зоны ( состояние р-типа) находятся в точке Г, дно верхней валентной зоны - в точке L. В точке Г три валентные р-зоны слипаются, в точках X и L вырождение частично снимается. [17]

Из приведенного рассмотрения следует, что существует много способов взаимодействия электронов с длинноволновыми фононами. В табл. 3.4 показаны различные типы взаимодействий для двух типичных полупроводников, полярного ( GaAs) и неполярного ( Si), для электронов в нижней зоне проводимости или в верхних валентных зонах. Отметим, что в то время как ТА фонон может создать только сдвиговую деформацию, но не приводит к объемному расширению, с LA фононом может быть связано и то, и другое. [18]

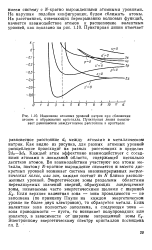Изменение атомных уровней натрия при сближении атомов и образовании кристалла. Пунктирная линия показывает равновесное междуатомное расстояние в кристалле. [19]

Каждый атом эффективно взаимодействует с соседними атомами в локальной области, содержащей несколько десятков атомов. Во взаимодействии участвуют все атомы металла, поэтому JV-кратное вырождение снимается и вместо дискретных уровней возникает система квазинепрерывных энергетических полос, или зон, каждая состоит из N близко расположенных уровней. Энергетические зоны разделены областями нереализуемых значений энергий, образующих запрещенные зоны, называемые часто энергетическими щелями с шириной Eg. Если верхняя валентная зона - зона проводимости - не заполнена ( по принципу Паули на каждом энергетическом уровне не более двух электронов), то образуется металл. Если валентная зона полностью заполнена, а следующая зона - зона проводимости - пуста, то возникает полупроводник или изолятор, в зависимости от ширины запрещенной зоны Eg. Электронному энергетическому спектру кристаллов посвящена гл. [20]

Страницы: 1 2