Адекватность - полученная модель
Cтраница 1
Адекватность полученной модели и необходимость ее коррекции оценивают чаще всего по критерию минимума среднеквадратичной ошибки. Этот метод наиболее целесообразен. [1]
Адекватность полученной модели оценивается по критерию Фишера. С помощью этого критерия определяется значимость различия дисперсий модели и опыта. Если различие незначимо ( при уровне значимости обычно 5 %), то гипотеза об адекватности модели может быть принята. [2]
Проверим адекватность полученной модели, сопоставив остаточную дис - персию (9.22) и дисперсию воспроизводимости. [3]
Для проверки адекватности полученной модели были использованы опыты в центре плана, когда все факторы поддерживались на основном уровне. [4]
Проверка нуль-гипотезы подтверждает адекватность полученной модели в рассмотренном диапазоне изменения факторов. [5]
На последнем этапе формулируется критерий адекватности полученных моделей и проверяется эквивалентность модели и системы. [6]
Выбор входных воздействий осуществляется для определения степени адекватности полученной модели, а не для идентификации объекта по его реакции на выбранное входное воздействие. Поскольку поведение сложных систем может быть описано в терминах параметров порядка, то выбор и использование входных сигналов производится, исходя из степени их влияния на параметры порядка и с целью верификации полученной модели. [7]
Регрессионный анализ устанавливает методы выбора степени и проверки адекватности полученной модели. [8]
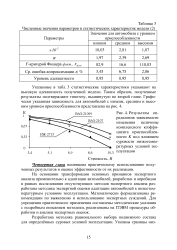 |
Численные значения параметров и статистических характеристик модели ( 2. [9] |
Указанные в табл. 3 статистические характеристики указывают на высокую адекватность полученной модели. Таким образом, полученные результаты подтверждают гипотезу, выдвинутую во второй главе. [10]
Регрессионный анализ устанавливает методы выбора степени полинома и проверки адекватности полученной модели. [11]
Регрессионный анализ устанавливает методы выбора степени полинома и проверки адекватности полученной модели. [12]
На третьем этапе выявляются параметры порядка, и формируется критерий адекватности полученных моделей. [13]
Ввиду того что kN и, следовательно, имеются лишние эксперименты, естественно проверить адекватность полученной модели (3.2.33) - например, с помощью Критерия Фишера. Это позволяет путем последовательных итераций выбрать такие факторы, которые дают адекватную модель при минимальном k, - искомые значимые факторы задачи. Теория и опыт показывают эффективность метода случайного баланса. [14]
Сравнение исходной vz и расчетной i2p характеристик движения рабочего органа привода подачи станка наглядно позволяет судить об адекватности полученной модели реальному объекту. [15]
Страницы: 1 2