Адекватность - полученная модель
Cтраница 2
 |
Принципиальная блок-схема структуры типовых процессов. [16] |
После того как на основе блочного принципа разработана полная математическая модель типового процесса химической технологии, на экспериментальной или промышленной установке проверяют адекватность полученной модели, корректируя в случае необходимости исходные параметры уравнений математического описания. [17]
После того, как на основе блочного принципа разработана полная математическая модель типового процесса химической технологии, на экспериментальной или промышленной установке проверяют адекватность полученной модели, осуществляя в - случае необходимости требуемую коррекцию исходных параметров уравнений математического описания. [18]
Построение математической модели включает следующие этапы: / - формализация изучаемого процесса, сбор и исследование информации, выбор определяющих параметров и каналов управления; 2 - построение и исследование математической модели; 3 - проверка адекватности полученной модели реальному процессу. [19]
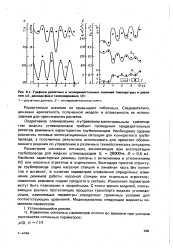 |
Графики расчетных и экспериментальных значений температуры и давления ( а, расхода фаз и газосодержания ( б. [20] |
Рассчитанные значения не превышают табличных. Следовательно, доказана адекватность полученной модели и возможность ее использования для практических расчетов. [21]
 |
Зависимость глубины проплавления Н и высоты факела Яф от тока фокусировки / ф вблизи точки оптимального режима. [22] |
Установленные математиматические модели линейны относительно контролируемых параметров. Оценки коэффициентов моделей о0, аь Ь0, bi получены по программе линейного регрессионного анализа REGRAN. Дисперсионным анализом подтверждена адекватность полученных моделей процессу в выбранной области режимов сварки и материалов. [23]
В настоящей главе рассматривается комплексный формализованный подход к реализации многоэтапной процедуры идентификации динамических объектов с использованием нейросетевых модельных структур. Нейро-сетевые методы идентификации рассматриваются как естественное развитие традиционной теории линейных систем, методов оптимизации функций многих переменных, нелинейной регрессии. Особое внимание уделяется практическим аспектам: созданию репрезентативной выборки экспериментальных данных и их предварительной обработке, рациональному выбору структуры нейросетевой модели, адаптации алгоритмов поиска минимума функций многих переменных к обучению нейронных сетей, проверке адекватности полученной модели, структурной оптимизации нейросетевых моделей с целью улучшения рабочих характеристик. В качестве основной задачи рассматривается построение логически законченной процедуры, позволяющей пользователю получить эффективные нейросетевые модели сложных нелинейных динамических объектов. [24]
При построении аналитической модели расчета неизбежны погрешности, которые возникают из-за недостаточности информации. Поэтому чаще используют экспериментальный метод, особенно в тех случаях, когда не известны необходимые зависимости для определения параметров струй. Это позволяет намного упростить сложные математические модели или заменить их более простыми аналитическими выражениями. Тот или иной метод при решении задачи выбирают исходя из конкретных условий и имеющейся априорной информации о параметрах пожарных струй. Вместе с этим любое математическое описание является лишь приближением к реальному процессу, а поэтому встает вопрос об адекватности полученной модели расчета и необходимости ее коррекции. Решение этого вопроса также возможно при проведении экспериментов, направленных на проверку основных параметров математического описания. [25]
При построении модели расчета неизбежны погрешности вследствие недостаточности информации. Поэтому чаще используют экспериментальный метод, особенно в тех случаях, когда неизвестны необходимые зависимости для определения параметров струй. Это позволяет намного упростить сложные математические модели или заменить их более простыми аналитическими выражениями. Вместе с этим любое математическое описание является лишь приближением к реаль-зюму процессу, а поэтому возникает вопрос об адекватности полученной модели расчета и необходимости ее коррекции. Реше-щие этого вопроса также возможно при проведении экспериментов, позволяющих проверить основные параметры математического описания. [26]
В случае эмпирических математических зависимостей для одного и того же типа процессов могут использоваться различные математические формулы, однозначные по точности. Например, формулы, вязкости неньютоновских жидкостей имеют не один десяток эмпирических зависимостей при погрешностях одинакового характера. Считается, что теория подобия в чистом виде неприменима к процессам, протекающим в элементах газопередачи, например, к процессам в аппаратах осушки газа сорбентами. Поэтому формульные эмпирические закономерности, полученные для лабораторных установок, нельзя без дополнительных исследований использовать, для расчета промышленных установок. Этот метод целесообразно применять при отсутствии априорной информации о структуре системы и физико-химических процессах, протекающих в ней, либо при оценке границ применимых аналитических методов, либо при большой сложности аналитического описания для получения более простых аналитических выражений. Адекватность полученной модели технологическим процессам и необходимость ее коррекции оценивается обычно критерием минимума средней квадратической погрешности. [27]
Страницы: 1 2