Малое начальное возмущение

Cтраница 2

Анализ устойчивости методом решения задачи Коши с помощью преобразования Лапласа позволяет не только найти область неустойчивости, но и проследить эволюцию во времени произвольного малого начального возмущения и получить информацию как о нарастании ( в неустойчивой области), так и о затухании возмущений. В частности, этот метод позволяет выяснить, насколько долго система помнит особенности возникшего в начальный момент времени возмущения. Вихревая часть возмущений заполняет поле течения горючего газа с конечной скоростью - скоростью движения продуктов горения относительно фронта пламени. Приход в рассматриваемую точку вихревого возмущения происходит через время hx / aun, где Дя - расстояние рассматриваемой точки от фронта пламени; исходное возмущение в этой точке сносится потоком. При этом величина вихря сносится без изменений, но возмущение скорости, вызванное этим вихрем, убывает по степенному закону, как и возмущение поверхности пламени. [16]

Из формулы ( 16 - 8) следует, что если мощность ГЭС Nr не превышает одной трети мощности системы Л Эс, то при бесконечно малых начальных возмущениях, отсутствии быстродействующего вторичного регулирования, отсутствии волновых процессов в каналах и потерь напора в трубопроводе на уравнительный резервуар не накладывается никаких ограничений. [17]

Не останавливаясь подробно на критике этого подхода, которой было уделено внимание в [92], отметим лишь, что рассматриваемый процесс симметричного деформирования в большинстве случаев окажется неустойчивым к малым начальным возмущениям несимметричного вида и оболочка не будет находиться в симметричном состоянии вплоть до упругой потери устойчивости. Интенсивное развитие несимметричных прогибов может начаться значительно раньше, и оболочка не доживет до бифуркации. [18]

Впервые строгая теория устойчивости нелинейных систем была предложена в 1892 г. А. М. Ляпуновым, который дал такое определение устойчивости ( устойчивость по Ляпунову): невозмущенное движение устойчиво, если при достаточно малых начальных возмущениях вызванное ими возмущенное движение сколь угодно мало отличается от невозмущенного; при этом движение асимптотически устойчиво, если при t - оо возмущенное движение стремится к невозмущенному. [19]

Если отклонения очень малы, то нелинейным членом ( содержащим х3) можно пренебречь; тогда обнаруживается неустойчивость системы вследствие эффекта отрицательного затухания, о котором шла речь еще в гл. Таким образом, сколь угодно малые начальные возмущения вызовут постепенно возрастающие колебания. [20]

Конечно, эта иллюстрация не является доказательством действительного существования турбулентного динамо; существуют еще и движения, дробящие масштабы поля. Для выяснения этого вопроса необходимо прямое исследование устойчивости турбулентного движения проводящей жидкости относительно малых начальных возмущений магнитного поля. Мы не будем излагать этих, достаточно сложных, исследований, а остановимся лишь на общем описании установившейся картины магнитогидродинами-ческой турбулентности в предположении существования турбулентного динамо. [21]

Конечно, эта иллюстрация не является доказательством действительного существования турбулентного динамо; существуют еще и движения, дробящие масштабы поля. Для выяснения этого вопроса необходимо прямое исследование устойчивости турбулентного движения проводящей жидкости относительно малых начальных возмущений магнитного поля. Мы не будем излагать этих, достаточно сложных, исследований, а остановимся лишь на общем описании установившейся картины магнитогидродинамической турбулентности в предположении существования турбулентного динамо. [22]

Система уравнений (3.41) не поддается аналитическому решению, но некоторые аналитические выводы из нее можно сделать без численных расчетов. Эта система имеет тривиальное решение с & e - k, ( с) 0, которое неустойчиво - малые начальные возмущения вида (3.46) экспоненциально нарастают. Это следует из линейной теории. [23]

Часы представляют собой классический пример систем, в которых колебательная часть существенно взаимодействует с источником энергии и образует вместе с ним единую специфическую автоколебательную систему. Характерной особенностью такой системы является наличие единственного режима стационарных колебаний, устанавливающегося при достаточно больших начальных отклонениях или начальных скоростях ( в случае достаточно малых начальных возмущений происходят затухающие колебания); иными словами, в часах осуществляется жесткое возбуждение автоколебаний. Другая особенность часов состоит в том, что передача энергии от источника энергии к колебательной части системы носит дискретный, импульсный характер, причем импульсы сообщаются колебательной части системы в некоторых фиксированных ее положениях. [24]

Если называть возмущенным движением движение с измененными начальными условиями, то устойчивость можно рассматривать как свойство возмущенного движения сколь угодно мало отличаться от невозмущенного при достаточно малых начальных возмущениях. Если к тому же движение при t - оо стремится к невозмущенному, то оно называется асимптотически устойчивым. [25]

При очень малых начальных возмущениях ( v С В) краевые условия (9.1) будут практически совпадать с краевыми условиями (8.1), причем в силу неравенства BL 0 течение будет неустойчивым. [26]

Для пространственно-однородного случая теорема существования доказана как для молекул-шаров 2), так и для псевдомаксвелловских молекул3) для полного нелинейного уравнения Больцмана. Однако существование решений доказано для времен тем меньших, чем больше начальная функция распределения отличается от равновесной. Таким образом, для времен макромасшгаба существование доказано лишь для малых начальных возмущений. [27]

Можно показать, что при больших отрицательных значениях х превосходящих по абсолютной величине Хо области, на которые отображают правую полуплоскость правая и левая части уравнения ( VIII. Такой стационарный режим является неустойчивым, причем нестационарные решения, соответствующие малым начальным возмущениям, удаляются от него путем колебаний с нарастающей амплитудой. [28]

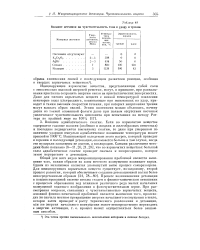Влияние песчинок на чувствительность тэна к удару и трению. [29]

Общей для всех видов микроинициирования проблемой является выяснение того, каким образом из зоны местного возмущения возникает взрыв. Одним из механизмов является упомянутый выше процесс саморазогрева. Процесс возникновения детонации в конденсированной системе весьма сходен в физико-химическом отношении с процессом образования под влиянием различного рода малых начальных возмущений видимого изображения в фоточувствительном зерне. [30]

Страницы: 1 2 3