Динамическое возмущение
Cтраница 3
Исследование динамических задач теории упругости в нелинейной постановке относится к одной из сложных и мало разработанных областей механики твердого деформируемого тела. В то же время существует целый класс задач, в которых на некоторое конечное напряженное статическое состояние накладываются малые динамические возмущения. Это позволяет в строгой постановке строить решение статической задачи, а динамику явлений, основываясь на малости динамических возмущений, исследовать на базе линеаризованных относительно некоторой малой окрестности напряженного состояния соотношений. При этом в полном объеме сохраняется присущая нелинейным задачам специфика постановки краевых задач в зависимости от используемой системы координат и используемых в процессе решения тензорных и векторных величин, описывающих напряженное состояние среды. [31]
Соотношения типа ( 36 11) являются точными в том смысле, что они не зависят от конкретных физических свойств рассматриваемой неравновесной системы. Таким образом, формула ( 36 12) определяет отклонение средних значений величин, характеризующих систему от их равновесных значений при воздействии на нее динамических возмущений. Поскольку усреднение в ФВА производится по состояниям равновесной системы, формула ( 36 12) позволяет найти значения средних для неравновесной по характеристике равновесной системы. Коррелятивная функция или, точнее, функция реакции, для рассматриваемых неравновесных систем играет ту же роль, что функция распределения для равновесных систем. [32]
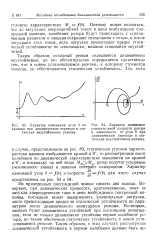
Мы видим, что здесь имеется ситуация, аналогичная во многих отношениях потере устойчивости сферических и цилиндрических оболочек в теории упругой устойчивости. В каждой области имеется нелинейная крайне неустойчивая бифуркация в триггерную моду, которая существенно отличается от достигаемого в результате динамического процесса конечного состояния и обнаруживает значительную чувствительность к несовершенствам и динамическим возмущениям; имеющееся на графиках отчетливо выраженное плато свидетельствует лишь о недостаточном уровне современного эксперимента. Действительно, единственная качественная разница между рис. 91 и приведенным выше рис. 25 гл. [33]
Причем по торцу призмы наносится ряд ударов с последовательно возрастающей энергией до отскока жесткого элемента. Таким образом, в материале призмы возникает плоская волна осевых напряжений, создающая однородное поле осевых динамических деформаций, нагружающих клеевой слой подобно полю деформаций в натурной конструкции, подвергнутой динамическому возмущению. [34]
 |
Технические данные малоинерционных двигателей серии ПГТ. [35] |
Основное отличие высокомоментных двигателей от обычных пазовых ДПТ заключается в замене электромагнитного возбуждения постоянными магнитами, что повлекло за собой существенное улучшение характеристик двигателей и приводов в целом. При этом высокомоментные двигатели сохранили достоинства обычных машин - высокую тепловую постоянную времени ( возможность значительных перегрузок по току в режимах кратковременной и повторно-кратковременной нагрузки), хорошее демпфирование ( малые чувствительность к динамическим возмущениям по нагрузке и колебательность двигателя в переходных режимах) и достаточную механическую прочность благодаря значительным размерам якоря и большому диаметру вала. [36]
Во-первых, при динамических процессах, кратковременно, пока не затухли апериодические токи в цепи возбуждения синхронной машины, последняя может выдерживать значительные нагрузки, часто превосходящие предел ее статической устойчивости по параметрам после динамического возмущения режима. Во-вторых, машина будет динамически устойчивой при постоянном возмущении, если не только динамически устойчиво первое колебание ротора, но также обеспечена статическая устойчивость в новом установившемся режиме. [38]
Поэтому выход машины за нормы геометрической точности не всегда приводит к потере ею качественных характеристик обработки. Тем не менее снижение геометрической точности, обусловленное износовыми и другими вредными медленно протекающими процессами, приводит к изменению траекторий движения исполнительных органов оборудования ( или заготовок при подвижном базировании) от расчетных законов движения и является источником дополнительных динамических возмущений, что не может не сказаться на точностных показателях обработки. Таким образом, контроль за показателями геометрической точности в процессе эксплуатации ( испытаний) может объективно свидетельствовать об ухудшении качества машины и, кроме того, позволяет получить информацию о возможных причинах этого ухудшения. [39]
Описан теневой оптический метод определения коэффициентов интенсивности Напряжений, который был применен при изучении динамически распространяющихся и затем останавливающихся трещин. Было использовано соотношение между диаметром каустики D и коэффициентом интенсивности / Ci, выведенное при допущении, что поле напряжений и деформаций у вершины трещины соответствует получаемому из статического решения. Точная формула в случае распространяющейся трещины, несомненно, может быть получена только с учетом динамического возмущения поля напряжений у конца трещины. Над получением такой формулы авторы работают в настоящее время. [40]
Исследование динамических задач теории упругости в нелинейной постановке относится к одной из сложных и мало разработанных областей механики твердого деформируемого тела. В то же время существует целый класс задач, в которых на некоторое конечное напряженное статическое состояние накладываются малые динамические возмущения. Это позволяет в строгой постановке строить решение статической задачи, а динамику явлений, основываясь на малости динамических возмущений, исследовать на базе линеаризованных относительно некоторой малой окрестности напряженного состояния соотношений. При этом в полном объеме сохраняется присущая нелинейным задачам специфика постановки краевых задач в зависимости от используемой системы координат и используемых в процессе решения тензорных и векторных величин, описывающих напряженное состояние среды. [41]
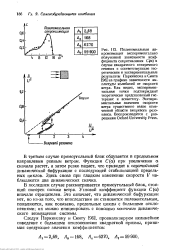
В последнем случае рассматривается прямоугольный блок, стоящий поперек потока ветра. Угловой коэффициент функции С ( а) вначале отрицателен. Это означает, что динамической бифуркации нет, но из-за того, что впоследствии он становится положительным, появляются, как показано, предельные циклы с большими отклонениями; их можно инициировать с помощью конечного динамического возмущения системы. [43]
Страницы: 1 2 3