Потенциальное возмущение

Cтраница 1

Потенциальные возмущения, сдвигающие пучности решений на периоде, имеют знакомый вид блоков ( барьер ямка) или ( ямка барьер) на каждую пучность решения, см. рис. 2.1. Только в общем случае собственные функции не имеют целого числа пучностей на одном периоде как в бесконечной прямоугольной яме. Это означает, что мы можем прецизионно управлять произвольной точкой Е спектра периодической структуры. [1]

В потенциальных возмущениях переменное магнитное поле значительно меньше электрического - ток проводимости и ток смещения почти полностью компенсируют друг друга. [2]

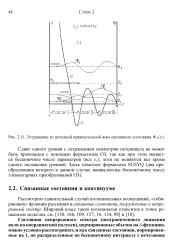Устранение из исходной прямоугольной ямы связанного состояния Фз ( ж. [3]

Рассмотрим удивительный случай потенциальных возмущений, собирающих функции рассеяния в связанные состояния, погруженные в непрерывный спектр. [4]

Полная проницаемость возникает при квазисвязанных состояниях и над одним прямоугольным барьером, ср. с а. Резонансы отчетливей проявляются в случае широких барьеров.| Резонансы проницаемости над прямоугольными ямами разной ширины. Пики резо-нансов, как и на, расположены на месте уровней соответствующей прямоугольной ямы с бесконечными стенками. Резонансы прозрачности над ямой на не требуют накопления волн в области ямы. [5]

Оказалось, что формы потенциальных возмущений для мнимых и действительных сдвигов энергий связанных состояний имеют качественное сходство. Замечательно, что и здесь годится обобщение правила, сформулированного нами в разделе 1 [18, 23], только теперь его можно применить к мнимой части потенциального возмущения. Уравнения Шредингера с комплексными потенциалами эквивалентны ( неэрмитовым. Нормировка сдвинутых состояний не сохраняется, потоки для падающей и уходящих волн становятся различными. [6]

Действительно, на рис. 4.3 а потенциальное возмущение имеет четыре, а на рис. е - пять бугорков для подъема четвертого ( пятого) уровня. [7]

Ej % Ej % - Вещественная часть потенциального возмущения оказывается при этом сравнительно малой. [8]

Выбирая начальное возмущение, мы получаем ту или иную амплитуду растущего потенциального возмущения. [9]

Векторное произведение отлично от нуля, если градиент давления в малом потенциальном возмущении не параллелен градиенту плотности. [10]

Это решение обобщает результаты теории возмущений и описывает эволюцию растущей моды потенциальных возмущений на нелинейном этапе. [11]

Рассмотренные возмущения могут, таким образом, оказаться растущими, как оказывались растущими потенциальные возмущения в изотропном мире. [12]

Раньше [18] мы, меняя силу сгребания только физических функций вспомогательной прямоугольной ямы, добивались разрыва ( соответствующими периодически продолженными потенциальными возмущениями) непрерывного спектра с порождением лакуны разной ширины при энергии избранного уровня. Но это было возможно лишь для дискретного множества точек, то есть множества меры нуль по сравнению континуумом энергетической шкалы. Только в последнее время нами было понято, что для периодических структур очень важно управление спектральными параметрами краевой задачи с произвольными однородными граничными условиями на концах интервала с шириной равной периоду. Хотя при каждом фиксированном наборе граничных условий мы имеем дискретный спектр собственных значений и функций, но, имея свободу выбора граничных условий из континуального множества, мы получаем возможность управлять спектральными параметрами в любой точке энергетической шкалы. [13]

В действительности флуктуации плотности, даже малые, порождают и соответствующее поле тяготения, иными словами, эти флуктуации являются начальными для дальнейшего роста потенциальных возмущений за счет гравитационной неустойчивости. Таким образом, этот предельный случай переходит на рельсы адиабатических возмущений. Отличие заключается в том, что начальное поле скоростей содержит вихревые составляющие. Поэтому вихревая скорость оказывается относительно малой. Теория слабой турбулентности лишена той главной привлекательной черты, ради которой вводится турбулентность. [14]

Давление в этих масштабах не играет роли, а характерное гидродинамическое время, th х: K / v, больше t, так что такие потенциальные возмущения нельзя рассматривать как звуковые волны. [15]

Страницы: 1 2 3