Скачкообразное возмущение

Cтраница 2

В процессе нагрева действуют скачкообразные возмущения до 20 % хода исполнительного механизма. [16]

Кривые разгона астатического объекта первого порядка. [17]

Следовательно, при воздействии скачкообразного возмущения на вход астатического объекта первого порядка его выходной сигнал изменяется с постоянной скоростью и не стремится к какому-либо новому установившемуся значению. При снятии возмущающего воздействия астатический объект первого порядка приходит в состояние равновесия. Однако его регулируемый параметр при этом сохраняет значение, которого он достиг к моменту окончания переходного процесса. Следовательно, состояние равновесия астатического объекта может наступить при любом значении регулируемого параметра, поэтому такие объекты называются нейтральными в отличие от устойчивых статических объектов. [18]

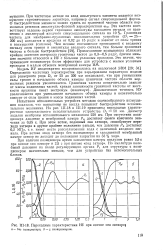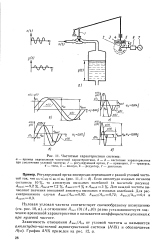
Переходные характеристики ИУ при потоке на затвор. о-без позиционера. б - s позиционером. [19]

Испытания исполнительных устройств методом скачкообразного возмущения показали, что позиционер не всегда повышает быстродействие исполнительного механизма. На рис. 111 - 18 и 111 - 19 приведены переходные характеристики односедельного исполнительного устройства Dy 50 мм. [20]

Частотные характеристики системы. [21]

Нулевая угловая частота соответствует скачкообразному возмущению ( см. рис. 10, а), а отношение Авых ( 0) / Л вх ( 0) равно установившемуся значению временной характеристики и называется коэффициентом усиления к при нулевой частоте. [22]

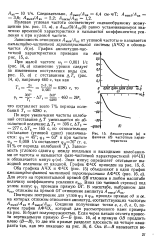Амплитудная ( а и фазовая ( б частотные характеристики. [23]

Нулевая угловая частота соответствует скачкообразному возмущению ( см. рис. 11, а), а ЛВЫХ ( 0) / ЛВХ ( 0) равно установившемуся значению временной характеристики и называется коэффициентом усиления к при нулевой частоте. [24]

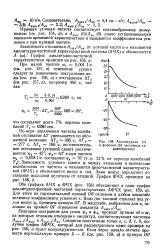Амплитудная ( а и фаЗовая ( б частотные характеристики. [25]

Нулевая угловая частота соответствует скачкообразному возмущению ( см. рис. 154, а), а Лвых ( 0) / ЛВХ ( 0) равно установившемуся значению временной характеристики и называется коэффициентом усиления к при нулевой частоте. [26]

Схемы прямоугольных импульсов. [27]

Для линейных объектов реакция на скачкообразное возмущение пропорциональна высоте скачка. [28]

Ранее были сопоставлены решения для скачкообразных возмущений. Такие сопоставления, как правило, учитывают амплитудные отклонения и не характеризуют сдвиг по фазе. С помощью гармонического возмущения можно наиболее полно оценить погрешность. [29]

Кривые разгона снимаются путем нанесения единичного скачкообразного возмущения параметра на входе в исследуемую систему, приведенную предварительно в состояние динамического равновесия, и записи кривой изменения параметра па выходе из системы. [30]

Страницы: 1 2 3 4 5