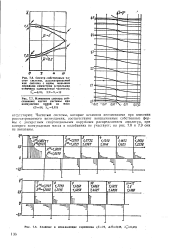
Рассматриваемое возмущение

Cтраница 1

Рассматриваемое возмущение имеет форму бегущей волны, называемой волной Тол-мипа - Шлихтинга. [1]

Рассматриваемое возмущение вызывает изменение не только состава первой части, но и химических потенциалов. [2]

Рассматриваемое возмущение движения вертолета определяется главным образом теми инерционными силами и моментами, которые возникают при отрыве лопасти несущего или рулевого винтов, причем наибольший интерес представ лйют только несколько секунд движения. Это дает возможность с допустимой степенью точности ограничиться линейной зависимостью аэродинамических сил и моментов, действующих на вертолет, от кинетических параметров движения и параметров управления. [3]

При рассматриваемом возмущении исходный круговой диск превращается в эллиптический. Как увидим ниже, условия стабилизации этой моды являются более трудными по сравнению с аксиально-симметричными ( коротковолновыми) возмущениями. [4]

Таким образом, рассматриваемые возмущения во всех случаях затухают со временем. [5]

Таким образом, рассматриваемые возмущения представляют собой гравитационные волны в расширяющемся мире. [6]

Это показывает, что рассматриваемые возмущения однородного потоки сосредоточены внутри конуса ( 161), который носит наименование конуса возмущений - конуса Маха. Угол раствора этого конуса 2а равен удвоенному углу возмущения ( углу Маха), подобно тому, как это имело место в плоском сверхзвуковом потоке. [7]

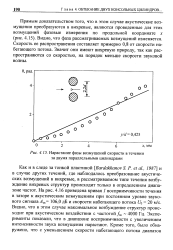Нарастание фазы возмущений скорости в течении за двумя параллельными цилиндрами. [8]

Видно, что фаза рассматриваемых возмущений изменяется. Скорость ее распространения составляет примерно 0 8 от скорости набегающего потока. Значит они имеют вихревую природу, так как распространяются со скоростью, на порядок меньше скорости звуковой волны. [9]

Давайте получим дисперсионное соотношение для рассматриваемых возмущений. [10]

Спектр собственных частот системы, рассматриваемой как система с вдвое меньшим порядком симметрии ( стрелками отмечены однократные частоты. 0 25. S / 2S, 12.| Изменение спектра собственных частот системы при возмущении одной из масс ( 524, А 0 0.| Главные и искажающие гармоники ( S24, ДЛГ0 48, . vc 0 25. [11]

Частотам системы, которые остаются неизменными при внесении рассматриваемого возмущения, соответствуют неискаженные собственные формы с дискретным синусоидальным окружным распределением амплитуд, при котором возмущаемая масса в колебаниях не участвует; на рис. 7.8 и 7.9 они не показаны. [12]

Заметим, что собственный параметр k не является инкрементом рассматриваемых возмущений, хотя ему и пропорционален. [13]

В результате решения соответствующей задачи будет получено описание развития рассматриваемого возмущения во времени и пространстве, которое, естественно, не должно зависеть от типа используемого разложения. [14]

Структурная схема системы регулирования.| Структурная схема комбинированной системы регулирования. [15]

Страницы: 1 2 3