Вековое возмущение

Cтраница 3

Пусть кваптовомохапич, система находится в стационарном состоянии, а энергия возмущения не зависит от времени. Эта задача аналогична учету вековых возмущений в классич, механике. Ожидается, что энергия ( частота) нач. Аналитически решение данной задачи выглядит след, образом. [31]

Влиянию сопротивления атмосферы посвящена работа Д. Е. Охоцим-ского, Т. М. Энеева, Г. П. Таратыновой Определение времени существования искусственного спутника Земли и исследование вековых возмущений его орбиты ( Успехи физических наук 63, № 1, 1957, стр. В этой же статье рассмотрены вековые возмущения, вызванные нецентральностью поля тяготения. [32]

В общем случае уравнений (5.3.6) ( при произвольных моментах сил, не имеющих силовой функции) также целесообразно применить метод осреднения для выявления основных эффектов движения. Этим способом, например, ниже будут исследованы вековые возмущения под влиянием моментов диссипативных сил, вызываемых аэродинамическим трением и вихревыми токами. [33]

При вычислении же этих интегралов рассматривают величины р, е, со как постоянные, ибо они за один оборот мало изменяются. Это значит, что постоянно накапливающимися изменениями ( вековыми возмущениями) величины со допустимо в первом приближении пренебречь; иначе говоря, можно считать, что со со0 const. Вычислив при таком предположении величины Ар и Де, мы найдем среднее изменение элементов р и е за один оборот спутника. [34]

V, 3 следует, что J не может испытывать никаких вековых возмущений. Дифференциальные уравнения для вековых возмущений величин j, иг, согласно гл. [35]

Оно называется также вековым уравнением и очень часто встречается в теории колебаний, теоретической и строительной механике, в аэродинамике, в небесной механике и играет большую роль в алгебре матриц. Вековым это уравнение называется потому, что к нему приводит в небесной механике задача исследования вековых возмущений планет. [36]

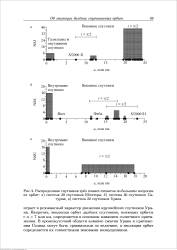Распределение спутников трех планет-гигантов по большим полуосям их орбит. а система 39 спутников Юпитера. б система 30 спутников Сатурна. в система 22 спутников Урана. [37]

Напротив, эволюция орбит далеких спутников, имеющих орбиты с а 7 млн км, определяется в основном влиянием солнечного притяжения. В промежуточной области влияние сжатия Урана и притяжения Солнца могут быть сравнимыми по величине, а эволюция орбит определяется их совместными вековыми возмущениями. [38]

Комбинируя таким образом попарно все планеты, можно определить возмущения их узлов и их взаимных наклонов, так как, согласно природе дифференциального исчисления, сумма частных значений дифференциала образует полное значение последнего. Таким именно образом были найдены годовые изменения узлов и наклонений планет, вызванные их взаимным притяжением, еще до того, как была создана прямая и общая теория вековых возмущений. [39]

В Memoires за 1782 г.) я применил эти уравнения к шести главным планетам, приняв для их масс наиболее вероятные значения, и отсюда путем интегрирования вывел общие формулы для возмущений их эксцентриситетов и мест их афелиев, которые дают значения этих элементов как для Земли, так и для других планет, по истечении любого неопределенного времени как до, так и после эпохи 1700 г. Так как, согласно этим формулам, эксцентриситеты остаются очень малыми, как мы это допустили, то при вычислении создается уверенность в их точности во все истекшие и будущие времена. Затем в томе за 1786 - 1787 гг. тех же Memoires, напечатанном в 1792 г., можно найти дополнение) ( supplement) к настоящей теории, касающееся новой планеты Гершеля [20], в котором тем же методом и тоже с помощью общих формул определяются вековые возмущения эксцентриситета и места афелия этой планеты, вызываемые влияниями Юпитера и Сатурна; при этом только оставлено без внимания влияние гершелевской планеты на упомянутые две планеты, равно как и на другие нижние планеты, ввиду незначительности ее массы и ее отдаленности. [40]

V, 3 следует, что J не может испытывать никаких вековых возмущений. Дифференциальные уравнения для вековых возмущений величин j, иг, согласно гл. [41]

Так как удалось провести только немного наблюдений новой планеты, то возникла проблема расчета орбиты планеты по малому числу наблюдений. Когда в 1802 г. был открыт второй астероид, Паллада, Гаусс заинтересовался проблемой вековых возмущений планет. [42]

Следовательно, во втором приближении величины Jf отличаются от постоянных не только на величины, которые в среднем, вычисленном ва приближенный период невозмущенного периода, обращаются в нуль, но также и на члены, возрастающие со временем. Если мы будем продолжать приближенное вычисление, то в качестве ю-го приближения получим, аналогично ( 24), выражение, в котором коэффициент при X представляется функцией от времени, содержащее кроме постоянных и периодических членов также и такие, в которых степени t до tn-i включительно умножены на постоянные или на периодические члены. Так получаются чисто вековые и смешанно вековые члены. В этом Ъмысле, сопоставляя результаты, можно сказать: при возмущении и-к р а т н о-п ериодичеокой невырожденной системы постоянные траекторий 7, не испытытывают вековых возмущений. Совсем иначе действует возмущение на траектории вырожденной системы. Предположим, что наша невозмущенная система с п степенями свободны w - кратно вырождена в смысле гл. Введем переменные состояния, определенные в заключении гл. [43]

Вековыми изменениями движения тел, например планетарных орбит, называют такие изменения, которые нарастают постепенно, в течение долгого времени ( saeculum - по латыни означает век, поколение), в противоположность изменениям, которые происходят быстро или периодически и не накапливаются. Какое, однако, все это имеет отношение к определению строения молекул. Дело в том, что вариационный метод можно связать с теорией возмущений и что в вариационном методе рассматриваются как раз те возмущения, которые накапливаются и дают набор орбиталей с определенными расстояниями между их энергетическими уровнями. Особенно четко это видно в теории возмущений для случая вырожденных состояний, с которой приходится сталкиваться ( не называя это столь сложным образом) в теории молекулярных орбиталей. Например, если рассматривается гомоядерная система, метод молекулярных орбиталей эквивалентен теории возмущений для вырожденных состояний. Действительно, в отсутствие взаимодействия между атомами все атомные орбитали с одинаковыми квантовыми числами, комбинации которых дают затем молекулярные орбитали, соответствуют одному и тому же вырожденному энергетическому уровню. Влияние межатомного1 взаимодействия подобно влиянию возмущения на эту вырожденную систему. Представим себе, что атомы расположены так же, как в молекуле, но взаимодействие между ними отсутствует, а затем будем постепенно включать взаимодействие. По мере накопления возмущения энергетические уровни различных линейных комбинаций атомных орбиталей будут расщепляться до тех пор, пока расстояния между ними не совпадут с имеющимися в молекуле. Таким образом, в этом случае мы действительно имеем дело с сильным вековым возмущением атомных орбиталей, а расстояние между уровнями можно найти с помощью векового определителя. [44]

Страницы: 1 2 3