Мелкомасштабное возмущение

Cтраница 2

Однако в связи с тем что используемые в настоящее время на практике методы определения не позволяют измерить весь спектр частот ( мелкомасштабными возмущениями обычно пренебрегают), приведенные ниже све дения носят в основном качественный характер. Согласно [25, 108, 197], при свободном отекании жидкости по вертикальной поверхности частота движения волн меняется в пределах 10 - 50 Гц. [16]

Если в маломощных лазерах задача сводится к выбору схемного решения на основе того или иного типа резонатора и каких-то особых физических сложностей обычно не возникает, то по мере увеличения энергетики лазера число проблем нарастает зачастую катастрофически: это и термооптические возмущения, и разного рода нелинейные процессы, включая само воз действия типа самофо-кусировочных, приводящие, в частности, к накоплению труднокорректируемых мелкомасштабных возмущений в лазерной системе. [17]

Волновые явления В воздушном потоке над горами возникают движения с горизонтальными масштабами 1 - 100 км, не считая характерных длинных волн, рассмотренных ранее ( с. Эти мелкомасштабные возмущения потока имеют очень большое значение для погоды непосредственно в районе их возникновения. [18]

Заметим, что в опытах регистрируются уже достаточно выросшие возмущения. Нелинейные эффекты для мелкомасштабных возмущений, которые играют определяющую роль в гидродинамической неустойчивости сферического пламени, проявляются значительно быстрее, чем для крупномасштабных, и поэтому даже возмущения, казалось бы, малой амплитуды могут обладать нелинейными свойствами. [19]

Устойчивость стационарного решения (2.97) указывает на устойчивость стационарного решения (2.87) к крупномасштабным возмущениям. Для исследования устойчивости к мелкомасштабным возмущениям необходимо рассматривать исходное уравнение (2.87) с распределенными параметрами. [20]

Итак, в широкой области изменения частоты столкновений электронов имеет место неустойчивость, связанная с убыванием магнитного поля наружу от шнура в область наружного обвода. Поскольку инкремент возрастает с fcj, то мелкомасштабные возмущения нарастают быстрее крупномасштабных, так что естественно ожидать турбулентной конвекции. Его зависимость от ve представлена на рисунке сплошной линией. [21]

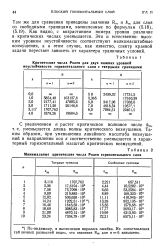Минимальные критические числа Рэлея горизонтального слоя. [22]

Как видно, с возрастанием номера уровня различие в критических числах уменьшается. Это и естественно: высоким уровням неустойчивости соответствуют мелкомасштабные возмущения, а в этом случае, как известно, спектр краевой задачи перестает зависеть от характера граничных условий. [23]

В случае когда уже на входе в усилитель возмущения попадают в полосу самофокусировочной неустойчивости, величина X L max становится функцией усиления С ехр ( а /) и ее вычисление усложняется. Он демонстрируется на рис. 6.1, где приведены зависимости нарастания мелкомасштабных возмущений в усилителе длиной 30 см [5] от пространственной частоты для разных усилений. [24]

В этот момент времени относительная величина амплитуды одной гармоники ( пп) проходит через минимум и начинает возрастать. Затем начинают расти соседние гармоники и фронт пламени начинает искажаться мелкомасштабными возмущениями, соответствующими номеру сферической гармоники 12 - 20, - развивается неустойчивость пламени. По мере дальнейшего роста пламени стабилизирующее действие кривизны пропадает и для более высоких сферических гармоник возмущения, и фронт сферического пламени приобретает относительно более мелкую структуру. [25]

В реальных условиях фронт горения в трубе обычно выпуклый по отношению к находящейся перед ним исходной газовой смеси. Это приводит к возникновению специфического механизма стабилизации пламени по отношению к мелкомасштабным возмущениям. [26]

С точки зрения создания условий для термоакустической самофокусировки света представляет интерес область параметров (4.50), для которой характерно перекрытие ( усреднение) акустических возмущений среды, в масштабе сечения пучка наряду с существованием локализованных температурных рассеивающих неоднородностей. Наконец, в области вида (4.51) температурные неоднородности перекрываются в пространстве между центрами тепловыделения, образуя мелкомасштабные возмущения показателя преломления, а также усредненную в сечении газовую линзу. [27]

Наличие воздушных промежутков между участками нелинейной среды, как мы видели в § 6.1, влияет на развитие мелкомасштабных возмущений. Это связано с тем, что промежутки вносят сдвиг фаз между пространственными гармониками cos ( xj /) ( r - поперечная координата) и основной волной - Дфх2 L / ( 2& 0) ( & - волновое число в воздухе, L - длина воздушного промежутка), а развитие возмущений, как отмечалось ранее, существенным образом зависит от Дер. Так, например, если Дфл: / 2, то возмущение, нарастающее в первом нелинейном элементе, затухает во втором. Казалось бы, это открывает возможность подавления ММС путем разделения среды па отдельные фрагменты, как это делается, например, в дисковом усилителе. Однако, как показывает анализ развития ММС [21, 41], такое разделение не позволяет снизить коэффициент передачи для всей области пространственных частот. Физически это связано с тем, что сдвиг фаз в воздушном промежутке приводит к затуханию возмущений на одних пространственных частотах, но к усилению возмущений на других. [28]

Скорость движения этого скачка относительно среды, однако, не равна ип, так как развившиеся к рассматриваемому моменту времени мелкомасштабные возмущения изменили его внутреннюю структуру. [29]

Поскольку уравнения Фридмана - Келлера оказываются всегда незамкнутыми, естественно возникает проблема замыкания уравнений для моментов. Основное-различие в поведении этих двух типов компонент турбулентности состоит в том, что крупномасштабные возмущения существенно зависят от геометрии потока и характера внешних воздействий, в то время как режим мелкомасштабных возмущений оказывается в значительной степени имеющим универсальный характер. Подробному разбору развития двух указанных направлений в теории турбулентности будут посвящены § 2 и 4 настоящего обзора. [30]

Страницы: 1 2 3