Синусоидальное возмущение

Cтраница 2

Обратим внимание на реакцию элемента на синусоидальное возмущение и укажем, что именно запаздывание создает сдвиг по фазе между выходной и входной величинами. Запаздывание следует рассматривать как неблагоприятное динамическое свойство реальных систем. [16]

Кривая D-разбие-ния, соответствующая величине перерегулирования. [17]

Пусть на вход нелинейного элемента подано синусоидальное возмущение с амплитудой А и частотой со. Тогда на выходе системы получим сложную периодическую функцию времени, содержащую весь спектр частот. Пользуясь разложением Фурье, можно определить амплитуды и фазы составляющих гармоник этой функции. [18]

При исследовании структуры потока известным методом синусоидальных возмущений проверка адекватности может осуществляться путем сравнения экспериментальных и теоретических зависимостей амплитудных и фазовых характеристик. Адекватность модели структуры потока может быть проверена также путем сравнения функций интенсивности. [19]

Выражение ( 32) состоит из трех синусоидальных возмущений. [20]

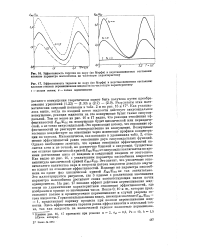
Графики распределения концентрации легколетучего компонента по высоте колонны. [21]

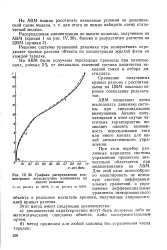
АВМ позволяют легко исследовать динамику системы при синусоидальном возмущении. Анализ получающихся в этом случае частотных характеристик позволяет оценить возможность использования того или иного канала для це лей автоматического управления. [22]

Эффективность тарелки по пару ( по Мэрфи в неустановившемся состоянии. влияние параметра массообмена на частотную характеристику.| Эффективность тарелки по пару ( по Мэрфи в неустановившемся состоянии. влияние степени перемешивания жидкости на частотную характеристику I - разрыв потока. 2 - полное перемешивание. [23]

Как указывалось выше, когда на входной поток жидкости действует синусоидальное возмущение, реакция жидкости на это возмущение будет также синусоидальной. Тем не менее из рис. 16 и 17 видно, что реакция отношения эф-фективностей EMv / Eoo на возмущение будет циклической или периодической, а не точно синусоидальной. Это происходит потому, что отношение эф-фективностей не реагирует непосредственно на возмущение. Возмущение косвенно воздействует на отношение через изменение профиля концентрации по тарелке. Математически, как показано в уравнениях табл. 2, отношение эффективностей равно отношению двух синусоидальных функций. Однако необходимо заметить, что кривая отношения эффективностей является хотя и не точной, но достаточно близкой к синусоиде. Существенное отличие циклической кривой EMV / EOG от синусоиды заключается во времени достижения пика от впадины и следующей впадины от этого пика. Как видно из рис. 16, с увеличением параметра массообмена возрастает амплитуда циклической кривой EMV / EQG - Это значит, что увеличение относительного количества пара и скорости потока жидкости довольно ощутимо влияет на отношение эффективностей. Влияние же параметра массообмена на сдвиг фаз циклической кривой EMV / EQG не так значительно. Это иллюстрируется рисунком, где 3 кривые с различными значениями параметра массообмена достигают своих соответствующих пиков почти одновременно. На рис. 17 показан эффект действия перемешивания жидкости на динамические характеристики отношения эффективностей, где изображены кривые со значениями числа Пекле 0; 10 и оо, которые представляют полное и промежуточное перемешивание и случай разрыва потока жидкости. Горизонтальная линия внизу, имеющая значение EMv / Eoo - 1, представляет картину процесса при полном перемешивании жидкости. Здесь эффективность тарелки равна эффективности в отдельной точке, так как жидкость на колпачковой тарелке полностью перемешана. [24]

Построение кривой разгона по импульсной характеристике.| Снятие частотных характеристик методом прямоугольной волны. [25]

Входной сигнал такого вида может быть представлен в виде суммы синусоидальных возмущений, определяемых разложением в ряд Фурье прямоугольной волны. [26]

Поведение аппаратуры регулирования было проверено в лаборатории путем подачи на вход синусоидальных возмущений и измерения амплитуды и фазы выходного сигнала. После изменений для улучшения некоторых приборов моделирование было проведено вновь. Затем система была смонтирована и, как и следовало ожидать, работала удовлетворительно с самого начала. [27]

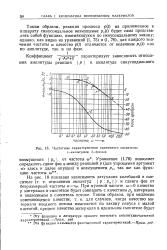Частотные характеристики единичного смесителя. У-амплитудная. 2-фазовая. [28]

Таким образом, реакция процесса p ( t) на приложенное к аппарату синусоидальное возмущение pn ( t) будет сама представлять собой функцию, изменяющуюся по синусоидальному закону; однако, как видно из уравнений ( I, 75) и ( I, 76), для каждого значения частоты со качество p ( t) отличается от величины рп ( 0 как по амплитуде, так и по фазе. [29]

Рассматривается самонастраивающийся экстремальный регулятор в виде аналогового вычислительного устройства, работающего по методу синусоидальных возмущений. Регулятор воздействует на расход воздуха, подаваемого в печь. Входным возмущением является расход газа. Максимизируется концентрация углекислого газа на выходе из печи. Для определения пределов устойчивости по коэффициенту усиления используется линеаризованная модель процесса и регулятора, параметрами которой являются чистое запаздывание процесса и коэффициент усиления. Для расчета потерь на поиск используются спектральная плотность входного возмущения и характеристики, заложенные в модель. Минимизируя потери на поиск, определяют оптимальное значение коэффициента усиления. Значения предела устойчивости и оптимального коэффициента усиления, найденные с помощью аналоговой модели, хорошо согласуются с величинами, экспериментально определенными на технологической установке. [30]

Страницы: 1 2 3 4 5