Синусоидальное возмущение

Cтраница 3

Проведенное исследование, строго говоря, позволяет утверждать только устойчивость прямолинейной формы по отношению к синусоидальным возмущениям. [31]

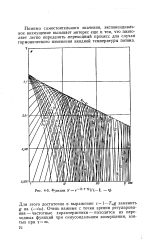Функция N. [32]

Очень важные с точки зрения регулирования - частотные характеристики - находятся из переходных функций при синусоидальном возмущении, взятых при т оо. [33]

Рассмотрены следующие типы возмущений: пилообразный импульс, ступенчатая функция, нарастающая функция, прямоугольный импульс и синусоидальное возмущение расхода. В первой графе табл. 1 показан закон изменения во времени массового расхода SQ ( 0 - Во второй графе приводятся изображения возмущений по расходу, в третьей-изображение величины запаса W ( s) для каждого типа возмущения. Оператор интегрирования 1 / s выражает динамическую характеристику процесса накопления. В последней графе таблицы даны графики изменения во времени величины накопления W ( t) n аналитиическое выражение этой функции. Начальное значение величины запаса W ( 0 принято равным нулю. [34]

Визуализация течения показала, что области, принимавшиеся в работе [38] за турбулентные пятна, состоят из двумерных синусоидальных возмущений большой амплитуды и наложенных на них высокочастотных колебаний. Иногда эти области исчезают, и устанавливается полностью ламинарное течение. Вниз по потоку частота появления турбулентных пятен возрастает, и наконец, ламинарное течение в слое разрушается. [35]

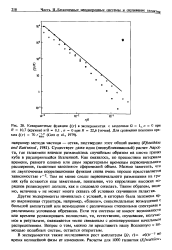Ковариантные функции. ( г в экспериментах с моделями П 1, п О при R 10 7 ( кружки и П. и 0 при R 22 6 ( точки. Для сравнения показана прямая. ( г 70 r -. ( Gott et al., 1979. [36]

Другие эксперименты начинались с условий, в которых была заложена ярко выраженная структура, например, блины, синусоидальные возмущения с большой амплитудой или возмущения с различными степенными спектрами и различными условиями обрезания. Если эти системы не имеют возможности или времени релаксировать полностью, то, естественно, скучивание, получаемое в результате, оказывается тесно связанным с доминирующим начальным распределением. Вопрос о том, можно ли представить нашу Вселенную с помощью подобных систем, остается открытым. [37]

Поскольку всякое начальное искривление фронта может быть разложено в ряд Фурье по синусоидам, достаточно рассмотреть только распространение синусоидального возмущения. [38]

О динамике дуги и ее постоянной времени 0Д судят по площади петли гистерезиса динамической ВАХ, полученной при малых синусоидальных возмущениях по току дуги на различных частотах. [39]

Чтобы проверить на устойчивость движущуюся границу раздела, последуем стандартной процедуре [37, 189] и предположим, что на прямую границу раздела наложено синусоидальное возмущение. [40]

Достоинством данного метода является большая точность определения параметров, а его недостаток состоит в том, что часто трудно для реального аппарата обеспечить синусоидальное возмущение. [41]

Если возмущение краев полосы, параллельных оси ж, носит более сложный характер, то, пользуясь рядами Фурье, его можно представить в виде суммы простых синусоидальных возмущений. [42]

Положив в ( 5 - 67) - и ( 5 - 68) - / ш и отделив в них мнимую часть, получим реакцию теплообменника на синусоидальное возмущение обогрева. Уравнение установившихся колебаний получается из ( 5 - 68) при т - - оо. [43]

К понятию амплитудно-фазовой частотной характеристики. [44]

Амплитудно-фазовой частотной характеристикой ( АФХ) системы или ее звена называется кривая ( рис. 87), которую описывает конец вектора выходной величины системы в режиме установившихся вынужденных колебаний при действии на ее входе синусоидального возмущения единичной величины и изменении частоты возмущения от 0 до со. [45]

Страницы: 1 2 3 4 5