Возникновение - параметрический резонанс
Cтраница 1
Возникновение параметрического резонанса в подобных системах связано с потерей устойчивости неподвижной точки соответствующего отображения Пуанкаре и поэтому обычно описывается линеаризованной в окрестности этой точки системой. [1]
Почему для возникновения параметрического резонанса амплитуда изменения параметра должна превышать некоторое пороговое значение. [2]
Полуцелые значения Q, и Q, запрещены из-за возникновения параметрического резонанса - резонансной раскачки колебаний, возникающей благодаря нерегу-лярностям градиента магн. [3]
Квазиконсервативная система (4.1) имеет две степени свободы: угол атаки а и угол собственного вращения ip, что создает предпосылки возникновения параметрического резонанса. Для проведения анализа резонансного движения эту возмущенную систему использовать нельзя, так как в ней явным образом не выражены частоты двух быстрых вращений. [4]
 |
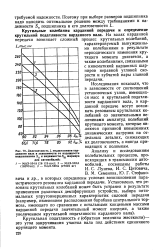
Влияние числа разноразмерных шариков [ в ] комплекте шарикоподшипника типа 76258 на спектры вибрации и шума двигателей. а - т0. б - т 1. в - от 2. [5] |
С увеличением номера гармоники круглограммы беговой дорожки кольца уменьшаются амплитуды переменных составляющих жесткости и статических нагрузок, действующих на элементы шарикоподшипника; при этом уменьшается возможность возникновения параметрических резонансов, что способствует уменьшению вибрации и шума. [6]
 |
Долговечность L подшипников карданного вала в зависимости от надежности подшипников Sn и надежности 5Щ шарнира для автомобилей. [7] |
Анализу и исследованиям колебательных процессов, происходящих в трансмиссии автомобилей, посвящены работы И. С. Лунева, И. С. Цитовича, В. М. Семенова, Ю. Г. Стефановича и др., в которых определены условия возникновения параметрического резонанса карданной передачи. [8]
Мозера доказал устойчивость стационарных решений почти для всех точек области, где выполнены лишь необходимые условия устойчивости, исследовал, используя методы осреднения, нелинейные колебания оси симметрии спутника в окрестности резонанса, рассмотрел возможность возникновения параметрического резонанса на эллиптических орбитах. [9]
Любая по величине внешняя сила может вызвать силовой резонанс. Для возникновения параметрического резонанса в неконсервативной системе величина воздействия должна быть больше некоторой пороговой величины. [10]
Стержень, нагруженный пульсирующей силой ( рис. 557, б), входит в параметрический резонанс также при частоте У, равной удвоенной частоте поперечных колебаний со. Условие возникновения параметрического резонанса в случае сжатого стержня часто называют условием динамической устойчивости стержня. [11]
В дальнейшем ограничимся, как уже отмечалось, первым приближением, что соответствует исследованию основного резонанса и позволит определить нижнюю границу динамической неустойчивости исследуемой системы. Так как при широкополосном спектре возмущений избежать возникновения основного параметрического резонанса невозможно, то такой вывод является вполне оправданным, а резонансы более высокого порядка для системы со случайными возмущениями в известной степени теряют смысл. Считаем, что время корреляции тк возмущений % и т ] значительно меньше времени релаксации тр амплитуды или фазы системы. Стохастические методы, связанные с использованием процессов Маркова, могут быть использованы при любом времени корреляции, если уменьшать интенсивность флюктуации возмущений, оставляя скорость ее изменения постоянной. [12]
Следует отметить, что этот метод позволяет исследовать параметрический резонанс любого порядка в зависимости от числа учитываемых членов разложения по малому параметру. Так как при широкополосном спектре возмущений избежать возникновения основного параметрического резонанса невозможно, то такой подход является оправданным, а ре-зонансы более высокого порядка для системы со случайными возмущениями в известной степени теряют смысл. Считаем, что время корреляции тк возмущений х0 ( t) и у0 ( t) значительно меньше времени релаксации тр амплитуды или фазы системы. [13]
Рассмотренная система с параметрическим возбуждением не является единственной в своем роде. Можно указать на целый ряд простых и сложных систем в которых возможно возникновение параметрического резонанса. На рис. 557 показано три таких примера. [14]
Если все числа 6, в, Т, и 7 2 заданы, то проверить это условие но представляет труда. Но останавливаясь на более подробном анализе неравенства (7.122), установим только условия возникновения параметрического резонанса при и. [15]
Страницы: 1 2