Возникновение - параметрический резонанс
Cтраница 2
Рассмотренная система с параметрическим возбуждением не является единственной в своем роде. Можно указать на целый ряд простых и сложных систем, в которых возможно возникновение параметрического резонанса. На рис. 558 доказано три таких примера. [16]
Поэтому для нелинейных систем ( в отличие от линейных) мы всегда имеем конечную амплитуду параметрически возбужденных колебаний опять-таки за счет неизохронности колебаний. В линейных же системах при осуществлении условия параметрического резонанса в любой из частотных областей резонанса будет происходить неограниченное нарастание амплитуды. При этом для возникновения параметрического резонанса в диссипативной системе необходимо, чтобы амплитуда воздействия ( глубина модуляции параметра т) была больше некоторого порогового значения, различного для разных частотных областей. [17]
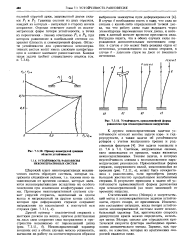 |
Пример невыпуклой границы области устойчивости.| Устойчивость прямолинейной формы равновесия при веконсервативном нагруженви. [18] |
Эти задачи освещены в гл. Системы, нагруженные силами, явно зависящими от времени, также являются неконсервативными. Таковы задачи, в которых неустойчивость связана с возникновением параметрических резонансов. Прямолинейная форма стержня, нагруженного силой, изменяющейся во времени ( рис. 7.3.11, в), может быть отождествлена с равновесием, если пренебречь ( ввиду большой жесткости) продольными колебаниями стержня. В результате приходим к задаче об устойчивости прямолинейной формы равновесия при неконсервативной ( но явно зависящей от времени) нагрузке. [19]
Резонанс при вынужденных колебаниях возникает при ш ш0 ( или ш ш0 / я с целым п при возбуждении короткими толчками), но сами колебания существуют при любой частоте внешнего воздействия. В случае параметрического воздействия колебания возникают лишь при выполнении соотношения ш 2ш0 / я. Резонанс при вынужденных колебаниях вызывает любая, сколь угодно малая внешняя сила. Для возникновения параметрического резонанса амплитуда внешнего воздействия должна превышать некоторое пороговое значение. [20]
Количество экспериментальных исследований, прямо или косвенно связанных с рассматриваемыми вопросами, невелико. В работе [108] приведены результаты опытов с маятником, движущимся в поле центробежных сил. Эти опыты позволили экспериментально получить движение, соответствующее периодическим решениям уравнения Матье и проверить существование областей неустойчивости. В работе [116] приведены результаты экспериментов, связанных с исследованием возникновения параметрического резонанса; эти эксперименты также производились с маятниками. Наконец, в [34] экспериментально показано, что в условиях вибрации точки подвеса неустойчивое положение равновесия маятника оказывается устойчивым. [21]
Страницы: 1 2