Слабая ударная волна
Cтраница 3
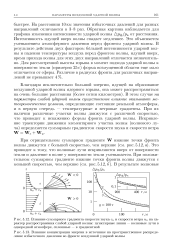
Рассматривается приближенный метод расчета распространения слабых ударных волн по покоящемуся политропному газу. Подробно исследован случай, когда появление ударной волны таким движением в газе криволинейного выпуклого цилиндрического поршня, что слабая волна начинает формироваться с нулевой начальной интенсивностью непосредственно на поверхности слабого разрыва, распространяющегося по области покоя. Приведены результаты численных расчетов. Предлагается приближенная аналитическая формула, описывающая затухание цилиндрической ударной волны. [31]
В этом случае на параметры слабой ударной волны существенное влияние оказывают метеорологические условия, определяющие состояние реальной атмосферы, и в первую очередь - температурные и ветровые градиенты. При их наличии различные участки волны движутся с различной скоростью, что приводит к искажению формы фронта ударной волны. [33]
При нагружении зарядов взрывчатого вещества слабыми ударными волнами ВВ ведет себя как инертная среда. Если предприняты специальные мероприятия по сохранению заряда от разрушения при нагружении ( например, заряд ВВ заключен в оболочку, которая не разрушается в результате нагружения), то удается исследовать структуру заряда ВВ после нагружения. При инертном поведении ВВ при исследовании микроструктуры сохраненных образцов не удается обнаружить видимых проявлений превращения ВВ. [34]
Как известно [7], в слабых ударных волнах приращения всех величин с точностью до членов второй степени по приращениям совпадают с приращениями в простой волне. Скорость ударной волны с той лее точностью равна полусумме характеристических скоростей до и после нее. Отсюда следует, что наличие слабой ударной волны не приводит к дополнительному по сравнению с непрерывным случаем изменению со временем интеграла f ficdx, и уравнение ( 13) остается справедливым. [35]
Проблема нерегулярного ( маховского) отражения слабых ударных волн, известная как парадокс Неймана, характеризуется тем, что классическая трехударная теория не позволяет адекватно описать структуру течения вблизи тройной точки. Впервые противоречия с классической трехударной схемой Неймана были выявлены в экспериментах [1] по дифракции скачка на клине. Эти и последующие эксперименты [2-7] показали, что для слабых падающих скачков с числами Маха Mi 1.5 решения по трехударной теории либо плохо согласуются с результатами эксперимента, либо не существуют. [36]
О Асимптотика ( 9) для слабых ударных волн совпадает ( по крайней мере по порядку величины) с соответствующей формулой [48], полученной эвристическим путем. [37]
Предположение о том, что при нагружении слабыми ударными волнами реакция протекает в форме горения, достаточно правдоподобно. [38]
Установим неравенства для скоростей, аналогично полученным для слабых ударных волн. [39]
Возможно, что и здесь промежуточным этапом между слабыми ударными волнами и нагревом короны является ионнозвуковая турбулентность. О такой турбулентности можно судить как по радиолокационным измерениям ( см. ниже), так и по другим данным, например, по немонотонному ходу яркостной температуры Солнца [ Каплан, Цытович ( 19676) ]: ионнозвуковая турбулентность, рассеивая радиоизлучение Солнца, может привести к появлению либо дополнительных максимумов либо дополнительных минимумов в стационарном его спектре. Пока ни наблюдательные данные, ни теоретические соображения не позволяют сделать уверенных заключений о распространенности и характере ионнозвуковой турбулентности в короне. Но вместе с тем гипотеза о значительной роли ионнозвуковой турбулентности во многих проявлениях солнечной деятельности также не противоречит ни наблюдательным данным, ни теоретическим соображениям. [40]
Прежде чем описывать результаты решения, напомним, что слабая ударная волна ( акустическая волна) при сферическом схождении усиливается по закону р - 1 / г независимо от уравнения состояния ваществзг. Таким образом, факт усиления слабой волны при схождении тривиален, однако он еще ничего не говорит о поведении волны перед центром. [41]
С во) - Рассмотрим простую теорию нерегулярного отражения слабых ударных волн, которая основана на упрощающем предположении ( Дж. [42]
При небольшом росте энтропии ( например, в случае слабых ударных волн) можно явно выразить сопротивление тела через изменение энтропии в потоке. [43]
Такая форма решения является в значительной степени универсальной для слабых ударных волн безотносительно к уравнению состояния среды с нормальными термодинамическими свойствами и диссипативных процессов, формирующих фронт. [44]
Более подробный анализ приводит к заключению, что в слабой ударной волне изменение энтропии AS пропорционально кубу амплитуды; AS - величина третьего порядка малости по отношению к давлению. [45]
Страницы: 1 2 3 4