Сферическая ударная волна

Cтраница 1

Для сферической ударной волны ( N 2), рассмотрение которой представляет наибольший интерес, были вычислены значения а для 7 7 / 5 и 7 3, при этом ai оказалось равным 0 717 и 0 638 соответственно. [1]

Закон движения фронта сферической ударной волны будет отличаться от закона движения фронта плоской ударной волны тем, что скорость фронта будет быстрее убывать с расстоянием; поэтому для равных промежутков времени длина сферической ударной волны будет меньше длины плоской ударной волны. [2]

Конструкция бесконтактного ударного возбудителя свободных колебаний. [3]

Рупор расширяет фронт сферической ударной волны, превращая ее в почти плоскую. Эта волна ударно возбуждает свободные колебания одновременно на значительной площади ОК, расположенного на расстоянии до 3 м от широкого конца рупора. [4]

Рассматривая условия в сферической ударной волне с реакцией, Жуге пришел к выводу, что здесь, в отличие от плоской детонационной волны, неизбежно непрерывное ослабление ударной волны и, следовательно, невозможен стационарный режим распространения [ 93, стр. Основным же отличием сферической детонационной волны от плоской является образование за фронтом волны бесконечно больших значений производных - др / дх, др / дх, ди / дх, в результате чего уже на малых расстояниях за фронтом можно ожидать конечных изменений этих величин. Это означает, что непосредственно за фронтом сферической детонации следует волна разрежения с резким спадом плотности, давления и скорости массового потока. [5]

В принципе теоретическое описание цилиндрических и сферических ударных волн одинаково. При этом были рассмотрены различные аспекты процесса. В простейшем случае в качестве модели была выбрана ударная волна, близкая к стационарной, с постоянной шириной зоны реакции, возникающая благодаря тому, что энергия, освобождаемая на большой площади зоны реакции, подводится к непрерывно уменьшающейся поверхности фронта волны. [6]

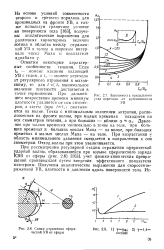Зависимость предельного.| Схема отражения сферической УВ от сферы. [7]

При рассмотрении регулярной стадии отражения сферической ударной волны, образовавшейся при взрыве сферического заряда КВВ от сферы ( рис. 2.8) [163], учет физико-химических превращений производился путем введения эффективного показателя изэнтропы, Получены аналитические выражения для скорости отраженной У В, плотности и давления вдоль поверхности тела. [8]

Распределение давления в rjae, по которому распространяется ударная волна. Пунктиром представлено начальное положение поршня. [9]

Количество вещества, захватываемое фронтом сферической ударной волны, возрастает при ее движении от точки взрыва. Поэтому сила сферической волны уменьшается с расстоянием гораздо быстрее, чем, например, сила образованной поршнем в трубе плоской волны. [10]

Схематическое изображение удар. [11]

На рис. 2.3 представлено графическое изображение сферических ударных волн от наземного взрыва ( Si) и надземного на высоте А над уровнем земли ( Sn); сфера 5Ш представляет собой отраженную волну при надземном взрыве, площадь этой сферы пропорциональна усилению - ударной волны в верхней части сферы Sn - При идеальном отражении ударных волн от земли при наземном взрыве вся энергия нижней полусферы переходит в верхнюю полусферу, удваивая ее плотность. Для конкретных условий падающая волна ( площадь сферы Sn) усиливается на величину площади отраженной сферы 5Ш, Соотношение площадей малой сферы 8щ и большой верхней Sn nSm / Sn (2.1) представляет собой отношение силы падающей ударной волны на твердую отражающую по-йерхность ( часто землю) к силе ударной волны верхней сферы. [12]

На рис. 2.3 представлено графическое изображение сферических ударных волн от наземного взрыва ( 5:) и надземного на высоте h над уровнем земли ( Su); сфера SIU представляет собой отраженную волну при надземном взрызе, площадь этой сферы пропорциональна усилению ударной волны в верхней части сферы Sn. При идеальном отражении ударных волн от земли при наземном взрыве вся энергия нижней полусферы переходит в верхнюю полусферу, удваивая ее плотность. Соотношение площадей малой сферы 5Ш и большой верхней Sn n Sm / Sn ( 2 1) представляет собой отношение силы падающей ударной волны на твердую отражающую поверхность ( часто землю) к силе ударной волны верхней сферы. [13]

Если принять гипотезу, что внутри фронта сферической ударной волны происходит одноосная деформация, то ударные адиабаты всегда ( даже при неголономном уравнении состояния) будут независимы от течения за фронтом, а решение задачи о структуре фронта волны позволяет получить дополнительные граничные условия. [14]

На самом деле приходится иметь дело со сферическими ударными волнами, процесс распространения которых существенно нестационарен и даже в простейших случаях требует для своего изучения применения сложного математического анализа. [15]

Страницы: 1 2 3 4