Упруго-пластическая волна
Cтраница 1
Распространение упруго-пластической волны на значительном расстоянии от поверхности нагружения, как и распространение волны в стержнях, практически не зависит от чувствительности материала к скорости пластического деформирования и удовлетворительно описывается деформационной теорией, не учитывающей вязкую составляющую сопротивления. На больших расстояниях от контактной поверхности скорость деформации на участке фронта пластической волны, прилегающем к упругому предвестнику, снижается практически до нуля, а крутизна фронта пластической волны уменьшается, не вызывая скоростной деформации материала при ее распространении. [1]
Распространение упруго-пластических волн в стержнях переменного сечения, Прикл. [2]
Распространение упруго-пластических волн в стержне с учетом влияния скорости деформации, Вычисл. [3]
Распространение упруго-пластических волн в стержнях переменного сечения, Прикл. [4]
Распространение интенсивных упруго-пластических волн, возбуждаемых импульсными нагрузками, характеризуется высокоскоростной деформацией материала в них, что позволяет изучать поведение материала при скоростях, не достижимых в квазистатических испытаниях. Вследствие зависимости сопротивления материала деформации от истории предшествующего нагружения сопоставление данных, полученных при исследовании волновых процессов, закон деформирования в которых определяется самой кинетикой деформации в волне, с результатами квазистатических испытаний с определенным параметром испытания невозможен без принятия определенной модели механического поведения материала. [5]
Особенности распространения упруго-пластических волн в стержнях с переменным пределом текучести, важные при изучении многократных ударов по стержню, рассматривались X. [6]
В отличие от упруго-пластической волны, ударная волна при распространении практически не изменяет крутизну фронта и, следовательно, процесс деформирования материала и его скорость при распространении волны сохраняются. [7]
Задача о распространении упруго-пластических волн в стержнях нес-сколько позднее рассматривалась независимо ( но без учета эффекта нагрузки) Дж. За этим последовал ряд обобщений на случаи разных начальных условий, переменного предела упругости по длине стержня и др. Все названные решения даны для упруго-пластического материала с упрочнением. [8]
В случае распространения слабой упруго-пластической волны, как показано на диаграмме ( х, t) волновых процессов при плоском соударении пластин ( рис. 118, а), в обе стороны от поверхности соударения распространяются центрированные волны сжатия, отражающиеся от свободных поверхностей в виде волн разгрузки С и С, симметричное взаимодействие которых формирует поле растягивающих напряжений. [10]
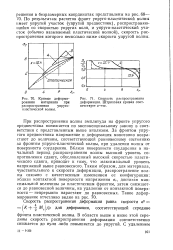 |
Кривые деформирования материала при распространении упруго-пластической волны.| Скорость распространения деформации. Штриховая кривая соответствует х - - оо. [11] |
По результатам расчетов фронт упруго-пластической волны имеет упругий участок ( упругий предвестник), распространяющийся со скоростью упругих волн, и упруго-пластический участок ( обычно называемый пластической волной), скорость распространения которого несколько ниже скорости упругой волны. [12]
Сопротивление сдвигу за фронтом упруго-пластической волны слабо зависит от интенсивности волны, что характеризует поведение материала, соответствующее идеальной упруго-пластической модели. [13]
Фиксируется выход на поверхность упруго-пластической волны сжатия и следующей за ней разгрузки. Небольшой гистерезис скорости объясняется гистерезисом цикла упругопласти-ческого деформирования. [14]
К настоящему времени развиты основы теории распространения упруго-пластических волн в одномерных случаях, главным образом в случаях продольных волн в стержне и полупространстве. [15]
Страницы: 1 2 3 4
