Упруго-пластическая волна

Cтраница 3

За пределами упругости зависимость a a ( e) для упруго-пластических сред имеет различный вид при нагружении и разгрузке. Задача о распространении упруго-пластических волн в полубесконечной среде при dza / d & 0 и в предположении, что разгрузка совершается по линейно упругому закону, впервые рассмотрена X. Если х - продольная координата, t - время, то в случае полубесконечной среды область ( х, t) делится на две части. В одной из них происходит нагру-жение, в другой - разгрузка. Трудность решения соответствующей системы двух гиперболических уравнений связана с тем, что граница между названными зонами, называемая волной разгрузки, заранее неизвестна. [31]

В области между этими точками напряжение достигает критической разрушающей величины в соответствии с некоторой кривой ВВ. Получение этой кривой для упруго-пластической волны не представляет затруднений, если в соответствии с экспериментальными результатами принять линейный закон изменения напряжений в волнах разгрузки. [32]

Аналогичная картина имеет место при выходе упруго-пластической волны на тыльную поверхность ударяющей пластины. [33]

Характер деформирования материала в плоской волне нагрузки определяется ее интенсивностью. При низкой интенсивности, Не превышающей предел упругости по материалу распространяется упруго-пластическая волна [298 - 300, 375, 385]; при высокой интенсивности возрастание объемной жесткости материала приводит к формированию ударной волны со скачкообразным изменением параметров на ее фронте. На фронте ударной волны достигается наиболее высокая скорость пластической деформации материала. [34]

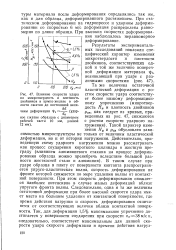Влияние скорости удара стом скорости удара соответству-на микротвердость и плотность ет более низкому деформацион-двойников в армко-железе в об - HQMy упрочнению ( микротвер. [35]

Яц и рдв обусловлен зависимостью микроструктуры не только от величины пластической деформации, но и от истории нагружения. В таком случае при ударе образца в плиту от поверхности контакта распространяется упруго-пластическая волна, скорость деформирования на фронте которой снижается по мере удаления волны от контактной поверхности. При этом скорость деформирования снижается наиболее интенсивно в случае малых деформаций вблизи упругого фронта волны. Следовательно, одна и та же величина остаточной деформации при более высокой скорости удара имеет место на большем удалении от контактной поверхности, где время действия нагрузки и скорость деформирования отличаются от соответствующих величин вблизи контактной поверхности. [36]

Указанному параметру испытания в пространстве aet соответствует плоскость aconst ( см. рис. 16, б), параллельная плоскости Eot, в которой лежит регистрируемая кривая е ( 0 - По своему характеру эта кривая аналогична обычной кривой ползучести ( см. рис. 16, г) и позволяет выявить особенности зарождения и развития малой пластической деформации в им-пульсно нагруженном материале. Испытания с таким параметром широко применяются для исследования явления задержки текучести [337] и закономерностей распространения упруго-пластических волн в стержнях. [37]

Наиболее высокие скорости деформации имеют место на фронте пластической волны, однако изучение пластического течения в них чрезвычайно затрудняется как необходимостью регистрации с наиболее высоким разрешением по времени ( порядка наносекунд), так и сложностью разделения упругих и пластических эффектов деформирования материала. Следует также напомнить о необходимости привлечения для анализа априорной модели материала и о слабой чувствительности профиля упруго-пластической волны к конкретной модели материала. [38]

При распространении волны амплитуда на фронте упругого предвестника понижается по экспоненциальному закону в соответствии с представленным выше анализом. За фронтом упругого предвестника напряжение и деформация монотонно возрастают до величины, соответствующей равновесному состоянию за фронтом упруго-пластической волны, при удалении волны от поверхности соударения. Вблизи поверхности соударения в начальный период распространения волны высокий уровень сопротивления сдвигу, обусловленный высокой скоростью пластического сдвига, приводит к тому, что максимальный уровень напряжений выше равновесного. Таким образом, для материала, чувствительного к скорости деформации, распространение волны связано с качественным изменением ее конфигурации: вблизи контактной поверхности напряжения ат, достигая максимальной величины за пластическим фронтом, затем снижаются до равновесной величины, на удалении от контактной поверхности - непрерывно нарастают до равновесных. [39]

С повышением скорости деформации обеспечение заданной равномерности деформации по длине образца связано с возрастающими трудностями. Поэтому естественной является попытка исследователей определить кривую деформирования материала при высоких скоростях деформации на основе анализа неравномерной деформации материала при распространении упруго-пластических волн нагрузки. Методы экспериментального определения полной кривой деформирования разработаны [228], однако исследования с использованием анализа волновых процессов в основном ограничиваются изучением влияния скорости деформации на предел текучести. [40]

Снижение относительного удлинения в области высоких скоростей деформации обусловлено локализацией деформации вблизи нагружаемого конца ( вследствие неравномерности деформирования по длине образца при распространении упруго-пластической волны), а не понижением пластичности материала. [41]

Это позволяет провести сопоставление процессов нагружения и деформирования. Точное определение скорости нагружения ( деформирования) является основным требованием, выполнение которого обеспечивает получение сопоставимых данных, хотя его определение связано с использованной для анализа моделью материала и теорией распространения упруго-пластических волн. [42]

Отсутствие удобного для анализа аналитического решения даже при использовании наиболее простого уравнения состояния, включающего вязкость, затрудняет получение ясного представления о связи характера деформирования материала под нагрузкой с закономерностями волновых процессов в стержнях. Экспериментально установленное распространение волн догрузки со скоростью упругих волн при растяжении ( сжатии) [239, 344, 377, 426] и кручении [25] подтверждает теорию Мальвер-на - Соколовского, в то время как многие эффекты, связанные с распространением упруго-пластических волн ( например, распределение остаточных деформаций по длине длинного стержня, постоянная скорость распространения деформаций и др.), удовлетворительно описываются деформационной теорией. [43]

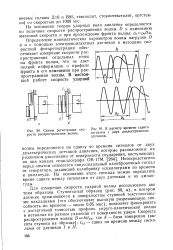Схемы регистрации скорости распространения волны.| К расчету времени сдвига сигналов с двух диэлектрических датчиков. [44]

Ступенчатый образец ( рис. 90, а), в котором датчики прижимаются к поверхностям ступеней текстолитовыми накладками ( что обеспечивает высокую разрешающую способность по времени - около 0 05 мкс), позволяет фиксировать с достаточной точностью профиль упруго-пластической волны в металлах на разном удалении от поверхности удара. [45]

Страницы: 1 2 3 4