Плоская гармоническая волна

Cтраница 2

Описывается характер распространения плоских гармонических волн в неограниченной среде. На примере неоднородного упругого стержня демонстрируется техника осреднения в динамических задачах. Далее эта техника применяется к пространственной динамической задаче теории упругости и линейной вязкоупруго-сти. Описывается явление волнового фильтра. Обсуждаются некоторые вопросы разрушения композитов. [16]

Мы ограничимся рассмотрением плоских гармонических волн малой амплитуды и проанализируем детально случай бесконечной проводимости. [17]

На рис. 4 изображена плоская гармоническая волна в два последовательных промежутка времени t и t At. Для наглядности можно представить, что это волна на поверхности воды, а Ф характеризует отклонение частиц поверхности воды от горизонтальной плоскости. Конечно, при такой интерпретации с является не скоростью света, а скоростью распространения волны относительно воды. Положительные значения Ф соответствуют горбам на поверхности воды, а отрицательные - впадинам. На рисунке изображена небольшая часть волны, включающая в себя два горба и одну впадину. [18]

Это есть дифференциальное уравнение плоской гармонической волны, распространяющейся по оси ОХ. [19]

Рассмотрим задачу о действии плоской гармонической волны сдвига на криволинейное отверстие. [20]

Применение условия нормировки к плоской гармонической волне де Бройля требует некоторой осторожности. В реальных условиях область движения микрочастицы У не может быть бесконечной, как это было бы для плоской гармонической волны. Поэтому обычно считают, что микрочастице сопоставляется почти гармоническая плоская волна де Бройля, которая совпадает с гармонической волной в достаточно большом объеме У0, а вне его быстро убывает. [21]

Если область, в которой распространяется плоская гармоническая волна - идеальный диэлектрик, то амплитуды векторов поля имеют постоянную величину. Затухание, которое имело бы место в случае конечной проводимости среды, не играет роли в поляризации. [22]

Рассмотрим теперь, что происходит, когда плоская гармоническая волна падает на поверхность раздела двух средин. [23]

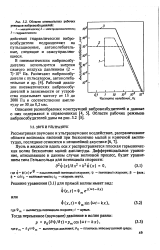Области оптимальных рабочих режимов вибровозбудителей. [24]

Пусть в жидкости вдоль оси х распространяется плоская гармоническая волна бесконечно малой амплитуды. [25]

Строгое решение нелинейной задачи сложения двух систем плоских гармонических волн с амплитудами аг и а2, частотами со1 и со2 распространяющихся в одном направлении в идеальной несжимаемой тяжелой жидкости ограниченной глубины Н, было развито Б. А. Дугиновым методом последовательных приближений Стокса [21 ] вплоть до членов второго порядка. Горизонтальная проекция орбитальной скорости, так же как в известном решении Стокса для регулярных волн конечной высоты [ см. формулы (2.20) - (2.22) ], включает стоксово течение. Как показано Б. А. Дугиновым, кинематические характеристики группы волн определяются суперпозицией кинематических характеристик двух составляющих систем волн. [26]

Следуя [42], рассмотрим задачу о действии плоской гармонической волны сдвига на жесткое цилиндрическое включение, сцепленное на части поверхности с упругой средой. [27]

Уравнение ( 67) имеет решения в виде плоских гармонических волн и соответствующее ему дисперсионное соотношение только в случае, если функция В ( х) либо постоянна, либо приближенно может считаться постоянной. [28]

В качестве основной связанной задачи термоупругости рассматривается распространение плоских гармонических волн расширения в неограниченном сплошном теле. Здесь для модифицированной под влиянием тепла упругой волны приводятся соотношения, выражающие изменение ее фазовой скорости, затухание амплитуды и относительное рассеяние энергии. [29]

Тем самым, если имеется ансамбль электронов, описываемый плоской гармонической волной де Бройля, абсолютно безразлично, проводить ли в этом случае измерения энергии и компонент импульса с одиночными электронами или с потоком одинаковых электронов. [30]

Страницы: 1 2 3