Альфвеновская волна

Cтраница 1

Неустойчивой оказывается альфвеновская волна с Ъг-ьт и и Ть ( поь / п0) соя. [1]

Групповая скорость альфвеновских волн направлена вдоль магнитного поля. [2]

При низких плотностях, там где частота альфвеновской волны велика, эти коды неустойчивы из-за использования явного интегрирования по времени. Для решения проблем, в которых существенны области с низкой плотностью или вакуум, необходимо вводить границу или применять другие стабилизирующие изобретения. Хьюетт [ Hewett, 1980 ] избавился от этих ограничений, решив одновременно систему связанных уравнений для электронов и ионов при помощи неитеративного неявного метода переменных направлений. [3]

Нетрудно установить, что частота свистящих атмосферик значительно превышает частоту альфвеновских волн и магнитного звука. [4]

При стремящихся к нулю Р, Т и ( vei) альфвеновская волна представляет собой низкочастотный предельный случай электромагнитных волн, распространяющихся в холодной плазме без потерь. При учете тепловых эффектов рассматривать затухание Ландау с помощью уравнений моментов невозможно; для анализа этого явления необходимо обратиться к уравнению Больцмаыа без столкновений. Эту задачу мы не рассматриваем. [5]

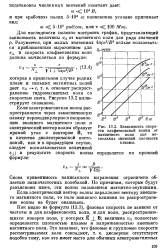Зависимость скорости альфвеновской волны от магнитного поля для нескольких значений плотности плазмы. [6]

Как видно из формулы (13.3), фазовая скорость не зависит от частоты и для альфвеновских волн, и для волн, распространяющихся поперек поля, у которых Е В; величина VA полностью определяется плотностью плазмы и напряженностью внешнего магнитного поля. [7]

Волны, переносящие возмущения магнитного поля, перпендикулярные к направлению постоянного магнитного поля В, называются альфвеновскими волнами. [8]

Величины af и as являются наибольшей и наименьшей скоростями распространения волн ( быстрых и медленных магнитозвуковых), а аА соответствует альфвеновским волнам. Собственное значение Я и соответствует энтропийным волнам. Представленный поход обеспечивает строгое упорядочение собственных значений. Он гарантирует отсутствие каких-либо их дополнительных нефизических вырождений, которые не присущи якобиевой матрице J. Отметим, что выбор других параметрических векторов s может, в принципе, нарушить это свойство. Кроме того, это имеет место если qy и qz не пропорциональны, соответственно, 7 и Z. В отличие от газовой динамики, в МГД-случае невозможно сконструировать матрицу А, зависящую от единого усредненного вектора. [9]

Величины af и 2S являются наибольшей и наименьшей скоростями распространения магни-тозвуковых волн ( быстрые и медленные МГД-волны), а аА соответствует альфвеновским волнам. Два совпадающих собственных значения Я и соответствуют волнам, переносящим энтропию и магнитный заряд. Предложенный подход обеспечивает строгое упорядочение собственных значений. Он гарантирует отсутствие их нефизического вырождения, которое не присуще исходной дифференциальной системе. [10]

Вверх по течению в квазипараллельной части ударного фронта имеется совершенно изотропная компонента частиц с энергией 100 кэВ и ларморовскими радиусами, сравнимыми с длиной альфвеновских волн. Кроме того, пучками электронов здесь генерируются ленгмюров-ские волны и вистлеры, а сверхтепловыми протонами - ионно-аку-стические волны. [11]

Член, описывающий питч-угловое рассеяние, стремится сделать изотропными частицы в системе отсчета, связанной с рассеивающими центрами, причем, в случае рассеяния на альфвеновских волнах, эта система по существу идентична системе покоя плазмы. Однако, часто оказывается более удобным использовать лабораторную систему, в которой плазма находится в движении. Поэтому, чтобы сохранить простую форму правой части уравнения (13.53), обычно пользуются смешанной системой фазово-пространственных координат с импульсом р, измеряемым в системе покоя плазмы, и пространственной переменной х7, измеряемой в лабораторной системе, в которой скорость плазмы, скажем, есть и. [12]

Для быстрых МГД ударных волн ( переход 1 - 2), как легко проверить с помощью (3.37), расходящимися являются медленная магнитозвуковая волна с амплитудой S k и альфвеновская волна с амплитудой АЦ за фронтом. [13]

Характер распада особой ударной волны, неэволюционной при учете диффузионных волн, детально не исследовался, здесь естественно воспользоваться аналогией с поведением контактных, тангенциальных, слабых и вращательных разрывов, которые: 1) относятся к особым, так как их скорость относительно газа совпадает с одной из характеристических скоростей - со скоростью энтропийных или альфвеновских волн; 2) являются поэтому неэволюционными при учете диффузионных энтропийных или альфвеновских волн. По-видимому, именно таким образом распадаются и неэволюционные особые ударные волны - не с образованием других волн или разрывов, а посредством диффузионного расплывания со временем. Кстати, неустойчивость этого типа не означает, что рассмотрение таких ударных волн и разрывов вовсе лишено смысла. Численный эксперимент, осуществленный для выяснения вопроса об устойчивости включающих ударных волн Г74 ], продемонстрировал, что слабом влиянии диссипаций ( в работе [74] их эффективно ла малая сеточная вязкость) включающая ударная волна устой чива. Этот результат косвенно подтверждает предположение том, что распад фронта включающей ударной волны идет за диссипаций указанным выше диффузионным образом. [14]

Страницы: 1 2 3