Стационарная детонационная волна
Cтраница 2
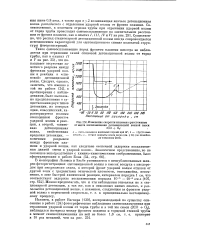 |
Изменение скорости пламени срасстоянием от места воспламенения детонационной волной смеси. [16] |
Существенно, что распад стационарной детонационной волны всегда сопровождается исчезновением характерной для детонационного спина полосатой структуры фоторегистраций. [17]
Знаменатель соотношения (3.72) вдоль всего фронта стационарной детонационной волны является положительной величиной. Распрямление линий тока происходит на слабой ветви ударной поляры. Координаты точки распрямления можно определить, приравняв числитель правой части (3.72) нулю. [18]
Знаменатель этого соотношения вдоль всего фронта стационарной детонационной волны является положительным. Распрямление линий тока происходит на слабой ветви ударной поляры. Координаты точки распрямления линий тока можно определить, приравняв числитель правой части (3.45) нулю. [19]
Мы установили, что снижение скорости стационарной детонационной волны, вызванное потерями, не может быть значительным. Однако это относится только к поведению детонационной волны в гладких трубах. [20]
Знаменатель этого соотношения вдоль всего фронта стационарной детонационной волны является положительным. При отсутствии разложения вещества I - ос на центральном участке фронта, соответствующем сильной ветви ударной поляры, числитель (9.41) является положительным, следовательно, R 0, т.е. линии тока поворачивают от оси заряда ВВ. Распрямление линий тока происходит на слабой ветви ударной поляры. Координаты точки распрямления линий тока можно определить, приравняв числитель правой части (9.41) нулю. Анализ соотношения (9.41), выполненный в [9.58], показывает, что если ширина зоны химической реакции мала по сравнению с радиусом кривизны фронта, то начальная кривизна линий тока вдоль фронта будет отрицательной, т.е. линии тока поворачивают к оси заряда в противоположность потоку без реакции. Это является важным результатом. [21]
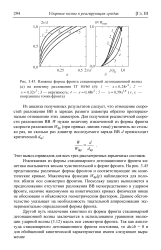 |
Влияние формы фронта стационарной детонационной волны ( а на кинетику разложения ТГ 40 / 60 ( б. 1 - х 0 24г. 2. [22] |
Другой путь извлечения кинетики из формы фронта стационарной детонационной волны заключается в использовании уравнения эволюции ударной волны (3.12) вдоль оси симметрии фронта. [23]
Наглядной демонстрацией отсутствия прямого влияния скорости реакции на свойства стационарной детонационной волны являются сравнительные измерения скорости детонации в сухих и влажных смесях окиси углерода с кислородом. [24]
В противоположность отсутствию какого-либо эффекта небольших добавок на скорость стационарной детонационной волны, было обнаружено резко выраженное действие добавок, заведомо не изменяющих термических свойств смеси, на условия возникновения детонации. [25]
Наглядной демонстрацией отсутствия прямого влияния скорости реакции на свойства стационарной детонационной волны являются сравнительные измерения скорости детонации в сухих и влажных смесях окиси углерода с кислородом. [26]
В противоположность отсутствию какого-либо эффекта небольших до-оавок на скорость стационарной детонационной волны, было обнаружено резко выраженное действие добавок, заведомо не изменяющих термических евойств смеси, на условия возникновения детонации. [27]
Эти значения скоростей детонации в цилиндре двигателя несколько превышают измеренную скорость стационарной детонационной волны в пентановоздушной смеси, равную при начальных атмосферных условиях около 1700 м / сек. [28]
Это совпадает с выводами теории идеальной детонации: разложение ВВ в зоне химической реакции стационарной детонационной волны сопровождается уменьшением давления и плотности среды. Предполагая как и ранее, что границей самоподдерживающего режима распространения детонации является равенство градиента давления ( а, следовательно, и градиента массовой скорости) нулю, из (3.49) можно получить условие прекращения стационарной детонации. Для этого определим значение градиента давления на оси симметрии заряда. [29]
Это совпадает с выводами теории идеальной детонации: разложение В В в зоне химической реакции стационарной детонационной волны сопровождается уменьшением давления и плотности среды. Предполагая, что границей самоподдерживающегося режима распространения детонации является равенство градиента давления ( а, следовательно, и градиента массовой скорости) нулю, из (9.45) можно получить условие прекращения стационарной детонации. Для этого определим значение градиента давления на оси симметрии заряда. [30]
Страницы: 1 2 3 4