Симметричная волна

Cтраница 1

Распадение тонких струй жидкости ( струи движутся. [1]

Симметричной волне ( 50) на поверхности струи отвечают ее последовательные расширения и сжатия. Волне 51, при которой смещения С пропорциональны cos б, отвечают такие деформации струи. [2]

Поперечное сечение круглого слоистого волновода с резис-гивными пленками. [3]

Для симметричных волн типа Е и Н в Л - слойном волноводе запись граничных условий приводит к 2 ( N-1) уравнениям относительно такого же числа постоянных интегрирования краевых задач либо Неймана, либо Дирихле. Для несимметричных волн из граничных услозий получаем 4 ( М-1) уравнений относительно 4 ( N-1) постоянных интегрирования обеих краевых задач. [4]

Образование симметричных волн элюирования зависит от-линейности равновесия. [5]

Схематическое изображение движения частиц среды в пластинах при распространении в них симметричной ( в и антисимметричной ( б воли Лэмба. стрелками показано направление смещений по осям х и г.| Зависимость фазовой е ( а и групповой е р ( б скоростей симметричных а и антисимметричных волн Лэмба различных порядков в пластине, отнесенных к скорости сдвиговых волн et, от величины fcjk-wft / cj. пунктирнан линия соответствует величине Сд с. [6]

В симметричных волнах движение частиц среды происходит симметрично относительно ср. БИыах пластины смещение и по оси х имеет одинаковые знаки, а смещение w по оси z - противоположные. В пластине толщиной 2h при частоте й может распространяться определ. [7]

Дисперсионные характеристики волны E0i круглого диэлектрического волновода, покрытого резистивной пленкой ( а, и частотные зависимости коэффициента замедления fj p /. o ( б при.| Зависимость коэффициента замедления от е диэлектрического волновода при Аа 5 - 10 - 4. [8]

При распространении симметричной волны в пленке протекают только продольные токи. [9]

В сферически симметричной волне перемещение каждой частицы является радиальным и представляет собой функцию времени и первоначального расстояния частицы от центра сферы. В несжимаемом теле условия несжимаемости определяют положения всех частиц при любом сферически симметричном движении, если задано положение какой-либо одной частицы. Здесь рассматриваются сжимаемые тела. [10]

Наряду с симметричными волнами в коаксиальной линии1 передачи могут существовать также волны несимметричного типа. [11]

Структуры полей и критическом режиме. [12]

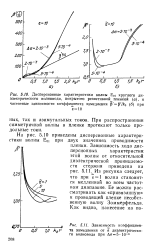
Таким образом, особенностью симметричных волн в круглом двухслойном волноводе с резнстивной пленкой является отсутствие в вышеуказанном смысле критических частот. [13]

Рассмотрим задачу о распространении сферически симметричных волн расширения, обусловленных скачкообразно изменяющимся во времени давлением, приложенным к поверхности сферической полости в бесконечной упругой среде. Приведем решение более общей задачи [56], считая среду сферически анизотропной ( центр анизотропии совпадает с центром полости) и неоднородной: модули упругости изменяются в зависимости от радиальной координаты по степенному закону с одним и тем же показателем степени. [14]

Радиальное распределение потока энергии для симметричных волн типа Н0 т и Е0т характеризуется отсутствием плотности потока на оси оптического волокна и в симметричных кольцевых областях, число которых равно т - 1, где т - номер волны. [15]

Страницы: 1 2 3 4