Спиновая волна

Cтраница 1

Спиновая волна, как всякое стационарное состояние, характеризуется энергией. Ее принято отсчитывать от энергии основного состояния. [1]

Аналогично спиновой волне сопоставляется частица, называемая магноном. [2]

Взаимодействие спиновых волн ( магнонов) с тепловыми колебаниями кристаллической решетки ( фононов) приводит к некоторому статистическому распределению спиновых волн с различными волновыми числами и направлениями. Амплитуды волн, возбуждаемых тепловым движением, очень малы. Непосредственное взаимодействие прецессии намагниченности с кристаллической решеткой сводится к элементарным процессам, при которых происходит уничтожение магнона с очень малым волновым числом и возникновение фонона. Однако вероятность этих процессов очень мала. Определяющую роль в передаче энергии спиновыми волнами играет двухступенчатый процесс, когда вначале происходит уничтожение магнона с fe 0 и возникновение магнона с k 0, а потом - уничтожение магнона с k; 0 и образование фонона. Расчет этого механизма потерь приводит к времени релаксации порядка 10 - 3 сек, что соответствует экспериментальным результатам для монокристаллов ферритов со структурой типа шпинели. [3]

Концепция спиновых волн, введенная в 1930 г. Блохом, оказалась очень плодотворной и в настоящее время широко используется в теории магнетизма. Это связано с тем, что знание характеристик энергетического спектра магнонов позволяет с помощью обычных формул статистической физики построить термодинамику магнитного кристалла. Задача о спектре магнонов достаточно точно может быть решена лишь при низких температурах, когда колебания намагниченности являются малыми. С другой стороны, именно эта область температур представляет особый интерес, поскольку при низких температурах теория молекулярного поля часто приводит к неправильным результатам. [4]

Спектр спиновых волн, который определяется выражением (5.85), показан на фиг. Для очень больших k член 4 л Л / sin20, который отражает влияние магнитных ддшольных сил на прецессию. [5]

Квантование спиновых волн приводит к квазичастицам, называемым магнонами. [6]

Частотная зависимость коэффициента поглощения света в Мпр2 в области экситон-магнонной полосы поглощения при Т2 2. К.| Зависимость молярного магнитного момента от магнитного поля в МпСОз при Г4 2 К.| Спектр АФМР в МпСО3 при Г4 2 К. а - сплошные кривые - поле приложено в базисной плоскости, пунктир - перпендикулярно. 1 - квазиантиферромагнит-ная ветвь колебаний. 2 - квазиферромагнитная ветвь ( возбуждается переменным магнитным полем, перпендикулярным постоянному. б - экспериментальные результаты для малых значений напряженности поля. [7]

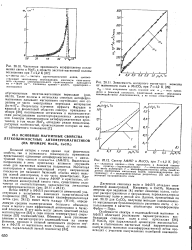
Дисперсия спиновых волн в АФЛП обладает определенной анизотропией. Например, в СоСО3 большую энергию при заданном k имеют спиновые волны, которые распространяются в направлении, перпендикулярном магнитному полю и легкой оси. Данные, приведенные на рис. 28.13 для СоСОз, получены методом одномагнонно-го мандельштам-бриллюэновского рассеяния света с использованием в качестве анализатора интерферометра Фабри - Перо. [8]

Релаксация спиновых волн при ферромагнитном резонансе в иттриевом гранате, не зависящая от состояния поверхности. [9]

Кванты спиновых волн называются магнонами [5, 6], они подчиняются статистике Бозе-Эйнштейна. [10]

Возбуждение спиновых волн происходит за счет энергии колебаний однородной прецессии. Это приводит к дополнительному затуханию однородной прецессии, проявляющемуся в расширении резонансной кривой. Спиновые волны с частотой сосп - со / 2, как следует из расчетов Сула, имеют при подмагничивающем поле, несколько меньшем резонансного, бесконечно большую длину волны. Этот результат свидетельствует о внутреннем противоречии в теории. Когда же длина волны становится соизмеримой с размерами образца, необходимо учитывать влияние его формы на структуру поля колебаний. [11]

LSW ( продольная спиновая волна, Ег), TSW ( поперечная спиновая волна, TbZn2) и SW ( промежуточный случай, Nd), Длина спинов в рассматриваемом случае модулирована вдоль ВВ k по простому закону, пакр. Поскольку значение атомного спина S ( - предполагается неизменным для каждого идентичного магн. [12]

Приложение теории спиновых волн к АФМ состоит в определении энергии S0 осн. [13]

При возбуждении спиновой волны в легкоосном АФМ атомные магн. Однако растворы конусов прецессии очень малы и различаются для рааных подрешеток, В случае АФМ др. симметрии движение атомных магн. [14]

Плотность состояний спиновых волн максимальна вблизи границы зоны Бриллюэна, поэтому максимум интенсивности рассеянного света для двухмагнонных процессов будет соответствовать удвоенной частоте магнонов с максимальными значениями волновых векторов вдоль направлений высокой симметрии. В этом случае нужно сравнивать частоту возбуждений с частотами, определенными методом рассеяния нейтронов, потому что для них получаются аналогичные условия. В табл. 5.5 приведены экспериментальные значения собственных частот магнонов, определенных различными методами для некоторых из изучавшихся магнито-упорядоченных кристаллов. Как правило, наблюдается хорошее согласие между частотами, измеренными разными методами. [15]

Страницы: 1 2 3 4